8) Teorema del Valor Intermedio

Clase 08: Teorema del Valor Intermedio

📚 Introducción

Esta clase presenta uno de los teoremas más importantes del cálculo: el Teorema del Valor Intermedio (TVI), también conocido como Teorema de Bolzano. Este resultado fundamental garantiza que las funciones continuas no pueden “saltar” valores, proporcionando una herramienta poderosa para demostrar la existencia de soluciones a ecuaciones y comprender el comportamiento de las funciones continuas.

Objetivos de la Clase

• Definir y comprender el Teorema del Valor Intermedio (TVI)
• Usar el teorema para determinar la existencia de raíces en una ecuación
• Aplicar el TVI en problemas prácticos y conceptuales
• Entender las limitaciones del teorema

---

1. Teorema del Valor Intermedio (Bolzano)

1.1 Enunciado del Teorema

Teorema del Valor Intermedio

Suponga que $f$ es continua sobre el intervalo cerrado $[a,b]$ y sea $N$ cualquier número entre $f(a)$ y $f(b)$, donde $f(a)\ne f(b)$.

Entonces existe un número $c$ en $(a,b)$ tal que $f(c)=N$.

1.2 Interpretación Geométrica

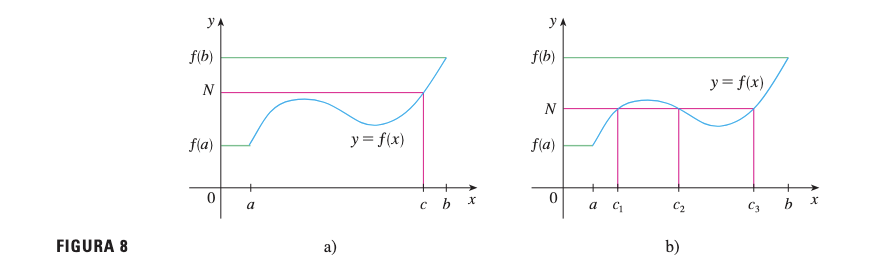
Interpretación Visual

El teorema establece que una función continua toma todos los valores intermedios entre $f(a)$ y $f(b)$. Geométricamente, si se traza cualquier recta horizontal $y=N$ entre $y=f(a)$ y $y=f(b)$, la gráfica de $f$ debe cruzar esta recta al menos una vez.

Observación Importante

• El valor $N$ puede tomarse una vez (como en la parte a) o más de una vez (como en la parte b)
• La función debe ser continua en todo el intervalo cerrado $[a,b]$
• El teorema garantiza existencia pero no unicidad

---

2. Aplicación Principal: Existencia de Raíces

2.1 Caso Especial para Raíces

Corolario - Existencia de Raíces

Si $f$ es continua en $[a,b]$ y $f(a)\cdot f(b)<0$ (tienen signos opuestos), entonces existe al menos un $c\in (a,b)$ tal que $f(c)=0$.

2.2 Ejemplo 1: Demostración de Existencia de Raíz

Problema: Demuestre que existe una raíz de la ecuación $4x^3-6x^2+3x-2=0$ entre 1 y 2.

Solución

Sea $f(x)=4x^3-6x^2+3x-2$

Paso 1: Verificar continuidad

• $f$ es un polinomio, por lo tanto es continua en todo $\mathbb{R}$
• En particular, es continua en $[1,2]$

Paso 2: Evaluar en los extremos

• $f(1)=4(1)-6(1)+3(1)-2=4-6+3-2=-1<0$
• $f(2)=4(8)-6(4)+3(2)-2=32-24+6-2=12>0$

Paso 3: Aplicar el TVI

• Como $f(1)<0<f(2)$ y $f$ es continua
• Por el TVI, existe $c\in (1,2)$ tal que $f(c)=0$

Conclusión: La ecuación tiene al menos una raíz en el intervalo $(1,2)$.

2.3 Localización más Precisa de Raíces

Método de Bisección

Podemos localizar la raíz con mayor precisión:

1. Evaluar $f(1.5)=f(1.5)\approx 0.25>0$
2. Como $f(1)<0$ y $f(1.5)>0$, la raíz está en $(1,1.5)$
3. Continuar subdividiendo para mayor precisión

---

3. Más Ejemplos de Aplicación

3.1 Ejemplo 2: Ecuación Trascendental

Problema: Demuestre que la ecuación $x+\tan (x)=2$ tiene al menos una solución en los reales.

Solución

Sea $f(x)=x+\tan (x)-2$

Estrategia: Buscar un intervalo donde $f$ cambie de signo

• Consideremos el intervalo $[0,\pi /4]$
• $f(0)=0+0-2=-2<0$
• $f(\pi /4)=\pi /4+1-2=\pi /4-1\approx -0.215<0$

Necesitamos buscar en otro intervalo:

• Probemos $[\pi /4,\pi /2)$
• A medida que $x\to (\pi /2{)}^{-}$, $\tan (x)\to +\infty$
• Por lo tanto, $f(x)\to +\infty$

Existe algún punto donde $f$ cambia de negativo a positivo, garantizando una solución.

3.2 Ejemplo 3: El Problema del Monje Tibetano

Problema: Un monje tibetano sale del monasterio a las 07:00 hrs y emprende su camino habitual hacia la cima de la montaña, a donde llega a las 7:00 PM. La mañana siguiente inicia el regreso desde la cima por la misma ruta a las 7:00 AM y llega al monasterio a las 7:00 PM.

Mediante el TVI demuestre que existe un punto a lo largo de la ruta que el monje cruzará exactamente a la misma hora en ambos días.

Solución Elegante

Modelación:

• Sea $s_1(t)$ = posición del monje el día 1 en el tiempo $t$ (7 AM = 0, 7 PM = 12)
• Sea $s_2(t)$ = posición del monje el día 2 en el tiempo $t$
• Ambas funciones son continuas (el monje no se teletransporta)

Función diferencia:

• Definamos $f(t)=s_1(t)-s_2(t)$
• $f(0)=s_1(0)-s_2(0)=\text{monasterio}-\text{cima}<0$
• $f(12)=s_1(12)-s_2(12)=\text{cima}-\text{monasterio}>0$

Aplicación del TVI:

• $f$ es continua (diferencia de funciones continuas)
• $f(0)<0$ y $f(12)>0$
• Por el TVI, existe $t_0\in (0,12)$ tal que $f(t_0)=0$
• Esto significa $s_1(t_0)=s_2(t_0)$

Conclusión: El monje pasa por el mismo punto a la misma hora ambos días.

---

4. Limitaciones del Teorema

4.1 Importancia de la Continuidad

El TVI Requiere Continuidad

El teorema NO se cumple para funciones discontinuas.

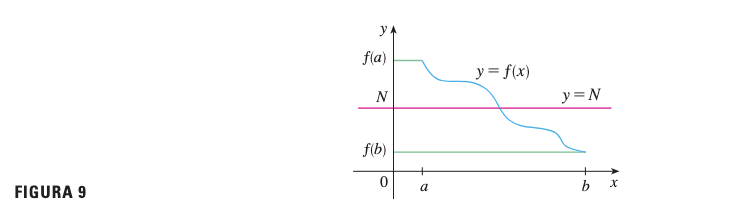
Contraejemplo

Una función discontinua puede “saltar” sobre el valor $N$ sin alcanzarlo nunca, violando la conclusión del TVI.

4.2 No Garantiza Unicidad

Múltiples Soluciones Posibles

El TVI garantiza al menos una solución, pero puede haber varias:

• La función puede cruzar la línea $y=N$ múltiples veces
• Para unicidad se necesitan condiciones adicionales (como monotonía)

---

5. Aplicaciones Computacionales

5.1 Visualización con Calculadora Gráfica

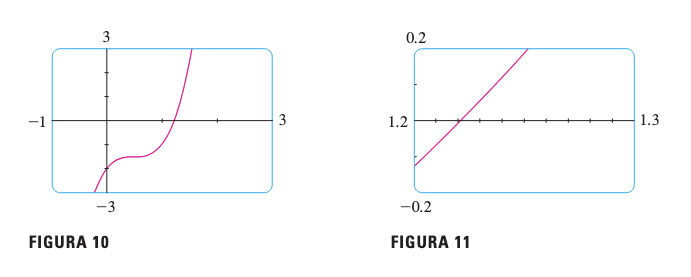
Uso de Tecnología

Las calculadoras gráficas y computadoras utilizan el TVI para:

• Graficar funciones continuas conectando puntos
• Encontrar raíces mediante métodos numéricos
• Detectar discontinuidades cuando el TVI falla

5.2 Método de Bisección

Algoritmo de Bisección

1. Comenzar con intervalo $[a,b]$ donde $f(a)\cdot f(b)<0$
2. Calcular punto medio $m=(a+b)/2$
3. Evaluar $f(m)$
4. Si $f(a)\cdot f(m)<0$, la raíz está en $[a,m]$
5. Si $f(m)\cdot f(b)<0$, la raíz está en $[m,b]$
6. Repetir hasta alcanzar precisión deseada

---

6. Ejercicio del Texto (Ejercicio 66)

Problema: Si $a$ y $b$ son números positivos, demuestre que la ecuación $\frac{a}{x^3+2x^2-1}+\frac{b}{x^3+x-2}=0$ tiene por lo menos una solución en el intervalo $(-1,1)$.

Guía de Solución

1. Definir $f(x)=\frac{a}{x^3+2x^2-1}+\frac{b}{x^3+x-2}$
2. Verificar que los denominadores no se anulan en $(-1,1)$
3. Establecer continuidad de $f$ en $[-1,1]$
4. Evaluar $f(-1)$ y $f(1)$
5. Mostrar que tienen signos opuestos
6. Aplicar el TVI

---

🎯 Conceptos Clave para Repasar

Resumen de Conceptos

1. TVI: Las funciones continuas toman todos los valores intermedios
2. Existencia de raíces: Cambio de signo implica raíz
3. Continuidad esencial: El teorema falla sin continuidad
4. Existencia vs unicidad: TVI garantiza existencia, no unicidad
5. Método de bisección: Aplicación práctica del TVI
6. Interpretación gráfica: No se pueden “saltar” valores

---

🚨 Errores Comunes

Error 1: Aplicar TVI a funciones discontinuas

• Incorrecto: Usar TVI sin verificar continuidad
• Correcto: Siempre verificar continuidad en $[a,b]$

Error 2: Asumir unicidad de la solución

• Incorrecto: El TVI garantiza exactamente una solución
• Correcto: El TVI garantiza al menos una solución

Error 3: Usar intervalos abiertos

• Incorrecto: Aplicar TVI en $(a,b)$
• Correcto: El teorema requiere intervalo cerrado $[a,b]$

---

📝 Ejercicios Propuestos

Ejercicios de Práctica

1. Probar que $x^5-3x+1=0$ tiene al menos una raíz real
2. Demostrar que $\cos x=x$ tiene solución en $[0,1]$
3. Usar el TVI para probar que toda función polinómica de grado impar tiene al menos una raíz real
4. Aplicar bisección para aproximar la raíz de $x^3-2=0$ con error menor a 0.01

---

📚 Referencias

Lectura Principal

• Sección 2.5: Continuidad, págs. 124-127

Sugerencia de Estudio

Se recomienda resolver el ejercicio 66 de la pág. 129. El TVI es fundamental para entender existencia de soluciones y será usado extensivamente en temas posteriores como el Teorema de Rolle y el Teorema del Valor Medio.

---

✅ Checklist de Estudio

Lista de Verificación

• Puedo enunciar el Teorema del Valor Intermedio
• Entiendo por qué la continuidad es esencial
• Puedo aplicar TVI para demostrar existencia de raíces
• Comprendo la diferencia entre existencia y unicidad
• Puedo usar el método de bisección
• Reconozco cuándo NO se puede aplicar el TVI
• Puedo resolver problemas conceptuales como el del monje

---

🏷️ Tags

calculo teorema-valor-intermedio TVI bolzano existencia-raices continuidad metodo-biseccion clase-08 clase