Clase 12: La Derivada como una Función
📚 Introducción
Hasta ahora hemos considerado la derivada de una función en un número fijo . En esta clase cambiamos la perspectiva: permitimos que el número varíe, convirtiendo la derivada en una nueva función . Este cambio conceptual es fundamental, ya que nos permite estudiar cómo cambia la razón de cambio a lo largo de todo el dominio de la función original. Además, exploraremos la importante relación entre continuidad y derivabilidad, y aprenderemos a identificar cuándo una función no admite derivada.
Objetivos de la Clase
- Determinar la fórmula y dominio de una derivada (como función)
- Conocer las notaciones para la derivada una función : , , ,
- Comprender la relación entre continuidad y derivabilidad:
- Derivable implica continua
- Discontinua implica no derivable
- Continua y no derivable (es posible)
- Identificar gráficamente cuándo una función no admite derivada: (1) discontinua, (2) esquina o punta, y (3) tangente vertical
- Determinar condiciones (parámetros) para que una función sea derivable en un punto
1. De la Derivada en un Punto a la Función Derivada
1.1 Recordatorio: Derivada en un Punto
En la clase anterior consideramos la derivada de una función en un número fijo :
1.2 La Derivada como Función
Ahora cambiamos el punto de vista y hacemos que el número varíe. Si en la ecuación anterior reemplazamos con una variable , obtenemos:
Definición - Función Derivada
La derivada de es la función definida por:
siempre que este límite exista.
Dado cualquier número para el cual este límite exista, asignamos a el número . De modo que consideramos a como una nueva función, llamada derivada de y definida por la ecuación anterior.
1.3 Dominio de la Derivada
Importante sobre el Dominio
El dominio de es el conjunto y puede ser menor que el dominio de .
2. Notaciones para la Derivada
2.1 Notaciones Principales
Si usamos la notación tradicional para indicar que la variable independiente es y la dependiente es , entonces algunas notaciones comunes para la derivada son:
Lectura de las Notaciones
- se lee “f prima de x”
- se lee “la derivada de f respecto a x”
- se lee “dy sobre dx” o “la derivada de y respecto a x”
2.2 Notación de Leibniz
Los símbolos y se llaman operadores de derivación porque indican la operación de derivación, que es el proceso de calcular una derivada.
La notación , introducida por Leibniz, no debe considerarse como una razón (por ahora); es sencillamente un sinónimo de . No obstante, es una notación útil y sugerente, especialmente cuando se usa en la notación de incrementos.
2.3 Valor de la Derivada en un Punto
Si deseamos indicar el valor de una derivada en la notación de Leibniz en un número específico , usamos la notación:
que es un sinónimo para .
3. Ejemplos de Cálculo de Derivadas
3.1 Ejemplo 1: Función Cuadrática
Problema: Si , encuentre una fórmula para .
Solución
Cuando se usa la ecuación 2 para calcular una derivada, hay que recordar que la variable es y que se considera temporalmente como una constante durante el cálculo del límite:
Por lo tanto:
3.2 Ejemplo 2: Función con Raíz Cuadrada
Problema: Si , encuentre la derivada de . Establezca el dominio de .
Solución
Racionalizamos el numerador:
Dominio de : Observe que existe si , de modo que el dominio de es y es menor que el dominio de , .
3.3 Ejemplo 3: Función Racional
Problema: Encuentre si .
Solución
Simplificando el numerador compuesto:
4. Interpretación Gráfica de la Derivada
4.1 La Gráfica de
Sabemos que el valor de en , puede interpretarse geométricamente como la pendiente de la recta tangente a la gráfica de en el punto .
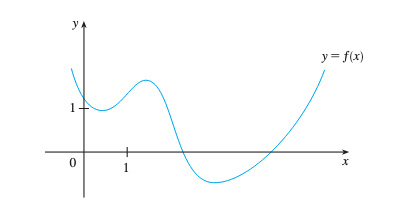
Cómo Graficar
f'a partir defPuede estimar el valor de la derivada, en cualquier valor de , trazando la tangente en el punto y estimando su pendiente. Por ejemplo, para , trace la recta tangente en de la figura y estime su pendiente alrededor de , por tanto, .
4.2 Ejemplo: Comparación de Gráficas
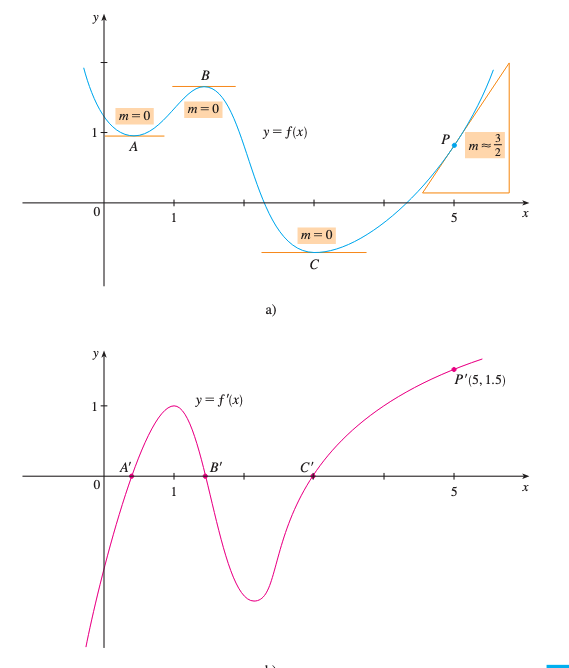
Observaciones de las Gráficas
- Donde tiene tangentes horizontales, (puntos , , )
- Entre y , las tangentes tienen pendiente positiva, por lo que
- Entre y , las tangentes tienen pendiente negativa, por lo que
- La gráfica de cruza el eje en los puntos , y directamente debajo de , y
5. Relación entre Continuidad y Derivabilidad
5.1 Teorema Fundamental
Teorema - Derivable Implica Continua
Si es derivable en , entonces es continua en .
DEMOSTRACIÓN: Para demostrar que es continua en , debemos demostrar que . Para esto empezamos por probar que la diferencia tiende a .
La información dada es que es derivable en ; es decir,
existe (véase la ecuación 2.7.5). Para relacionar lo dado con lo desconocido, divida y multiplique por (lo cual es posible cuando ):
De este modo, si usamos la ley del producto y la ecuación (2.7.5), podemos escribir:
En consecuencia, es continua en .
NOTA: El inverso del teorema 4 es falso
Es decir, hay funciones que son continuas, pero que no son derivables. Por ejemplo, la función es continua en porque:
(Véase el ejemplo 7 de la sección 2.3.) Pero en el ejemplo 5 demostramos que no es derivable en .
5.2 Tres Formas en que una Función No es Derivable
¿Cómo deja de ser derivable una función?
Si la gráfica de una función tiene “esquinas” o “picos”, la gráfica de no tiene recta tangente en esos puntos y no es derivable allí. [Al intentar calcular , encontramos que los límites por la izquierda y por la derecha son diferentes.]
El teorema señala otra forma en que una función no tiene derivada. En él se afirma que si no es continua en , entonces no es derivable en . Por ende, en cualquier discontinuidad (p. ej., una discontinuidad de salto), no es derivable.
Una tercera posibilidad es que la curva tenga una recta tangente vertical cuando ; es decir, es continua en y
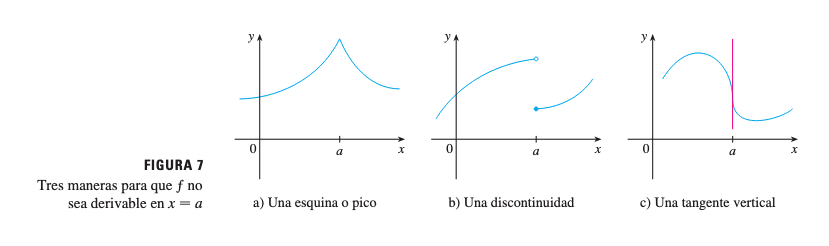
Tres maneras para que
fno sea derivable enx = a
- Una esquina o pico
- Una discontinuidad
- Una tangente vertical
6. Derivabilidad en un Intervalo
6.1 Definición
Definición - Derivable en un Intervalo
Una función es derivable en si existe. Es derivable sobre un intervalo abierto [o o o ] si es derivable en todo número del intervalo.
6.2 Ejemplo: Función Valor Absoluto
Problema: ¿Dónde es derivable la función ?
Solución (ya vista en Ejemplo 5)
Si , entonces y podemos elegir lo suficientemente pequeño de modo que , de aquí que . Por tanto, para tenemos:
y, por consiguiente, es derivable para cualquier .
De manera análoga, para se tiene que y se puede elegir lo suficientemente pequeña para que y, así, . Por tanto, para :
así que es derivable para cualquier .
Para debemos investigar:
(si existe). Calcule por separado los límites por la izquierda y por la derecha:
Puesto que estos límites son diferentes, no existe. Así, es derivable en toda , excepto en .
La fórmula para está dada por:
y su gráfica aparece en la figura. La inexistencia de se refleja geométricamente en el hecho de que la curva no tiene recta tangente en .
7. Determinación de Parámetros para Derivabilidad
7.1 Ejemplo con Parámetros
Problema: Determine y para que sea derivable en :
Solución
Para que sea derivable en , primero debe ser continua en :
Continuidad:
Para continuidad: … (ecuación 1)
Derivabilidad:
Usando que :
Para derivabilidad: … (ecuación 2)
De las ecuaciones 1 y 2: y
🎯 Conceptos Clave para Repasar
Resumen de Conceptos
- Función derivada: para cada donde existe el límite
- Dominio de : Puede ser menor que el dominio de :
- Notaciones: , , , ,
- Derivable implica continua: Si es derivable en , entonces es continua en
- Continua NO implica derivable: Ejemplo: es continua pero no derivable en
- Tres casos de no derivabilidad: esquina/pico, discontinuidad, tangente vertical
🚨 Errores Comunes
Error 1: Confundir
f'(a)conf'(x)
- Incorrecto: Pensar que son lo mismo
- Correcto: es un número (derivada en un punto), es una función
Error 2: Asumir que continua implica derivable
- Incorrecto: “Si es continua en , entonces es derivable en ”
- Correcto: Derivable Continua, pero NO al revés
Error 3: Olvidar verificar continuidad antes de derivabilidad
- Incorrecto: Solo verificar que los límites laterales de la derivada coinciden
- Correcto: Primero verificar continuidad, luego derivabilidad
Error 4: Pensar que
\text{Dom}(f') = \text{Dom}(f)siempre
- Incorrecto: Asumir que tienen el mismo dominio
- Correcto: (puede ser estrictamente menor)
📝 Ejercicios Propuestos
Ejercicios de Práctica
- Si , encuentre usando la definición
- Calcule la derivada de y determine su dominio
- Grafique si la gráfica de es la que se muestra (use tangentes)
- Determine y para que sea derivable en :
- Explique por qué no es derivable en
📚 Referencias
Lectura Principal
- Sección 2.8: La derivada como una función, págs. 154-159
Enlaces Relacionados
- 11) Razón de Cambio Promedio y Razón de Cambio Instantánea - Clase anterior
- Derivada-como-Funcion
- Continuidad-y-Derivabilidad
- Dominio-de-la-Derivada
Sugerencia de Estudio
Enfatizar la diferencia entre la derivada en un punto (número) y la función derivada, así como la relación entre ambas. Es fundamental comprender que . Practicar el cálculo de derivadas por definición para funciones como , , y funciones definidas por partes. El teorema “derivable implica continua” es crucial, pero recordar que el recíproco es FALSO.
✅ Checklist de Estudio
Lista de Verificación
- Puedo calcular usando la definición para diversas funciones
- Entiendo la diferencia entre (número) y (función)
- Conozco todas las notaciones de la derivada y cuándo usar cada una
- Comprendo que y puedo determinarlo
- Sé que derivable implica continua, pero NO al revés
- Puedo identificar gráficamente los tres casos de no derivabilidad
- Sé determinar parámetros para que una función por partes sea derivable
- Puedo graficar aproximadamente si tengo la gráfica de
🏷️ Tags
calculo derivadas funcion-derivada continuidad-derivabilidad dominio-derivada notacion-leibniz derivable-continua esquina-punta tangente-vertical clase-12 clase