13) Intro a Transformaciones Lineales

Clase 13: Introducción a las Transformaciones Lineales

---

Resumen Ejecutivo

Objetivos de la Clase

En esta clase aprenderás a:

• Comprender el concepto de transformación lineal
• Identificar transformaciones lineales geométricas básicas
• Verificar si una transformación es lineal
• Relacionar transformaciones con multiplicación matricial
• Analizar propiedades fundamentales de transformaciones lineales

Idea Central

Las transformaciones lineales son funciones especiales entre espacios vectoriales que preservan las operaciones de suma vectorial y multiplicación escalar. Estas transformaciones unifican y generalizan muchos conceptos del álgebra lineal, desde sistemas de ecuaciones hasta cambios de coordenadas.

---

1. Concepto de Transformación

1.1 Motivación

¿Por Qué Estudiar Transformaciones?

En matemáticas y aplicaciones, frecuentemente necesitamos:

• Transformar vectores de un espacio a otro
• Rotar, reflejar o escalar figuras geométricas
• Cambiar sistemas de coordenadas
• Modelar procesos físicos dinámicos

Las transformaciones lineales proporcionan el marco matemático para todas estas operaciones.

1.2 Definición de Transformación

Definición - Transformación o Mapeo

Una transformación (o función o mapeo) $T$ de ${\mathbb{R}}^n$ a ${\mathbb{R}}^m$ es una regla que asigna a cada vector $\mathbf{x}$ en ${\mathbb{R}}^n$ un vector $T(\mathbf{x})$ en ${\mathbb{R}}^m$.

Notación: $T:{\mathbb{R}}^n\to {\mathbb{R}}^m$

Terminología:

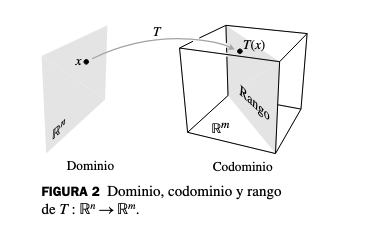
• ${\mathbb{R}}^n$ es el dominio de $T$
• ${\mathbb{R}}^m$ es el codominio de $T$
• $T(\mathbf{x})$ es la imagen de $\mathbf{x}$ bajo $T$
• El conjunto de todas las imágenes $T(\mathbf{x})$ es el rango de $T$

1.3 Notación y Visualización

Diagrama Conceptual

---

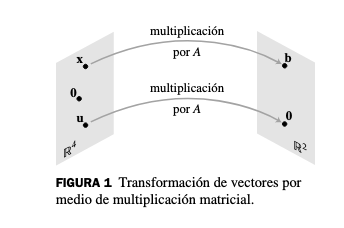
2. Transformaciones Matriciales

2.1 Definición

Definición - Transformación Matricial

Para cada $\mathbf{x}$ en ${\mathbb{R}}^n$, $T(\mathbf{x})$ se calcula como $A\mathbf{x}$, donde $A$ es una matriz $m\times n$. A veces esta transformación matricial se denota como $\mathbf{x}\mapsto A\mathbf{x}$.

Propiedades:

• El dominio es ${\mathbb{R}}^n$ (cuando $A$ tiene $n$ columnas)
• El codominio es ${\mathbb{R}}^m$ (cuando cada columna de $A$ tiene $m$ entradas)
• El rango es el conjunto de todas las combinaciones lineales de las columnas de $A$

2.2 Ejemplo Básico

Ejemplo 1 - Transformación Simple

Sea $A=\left[\begin{array}{cc}1& -3\\ 3& 5\\ -1& 7\end{array}\right]$ y sea $\mathbf{u}=\left[\begin{array}{c}2\\ -1\end{array}\right]$.

Calcular $T(\mathbf{u})$ donde $T(\mathbf{x})=A\mathbf{x}$:

$T(\mathbf{u})=A\mathbf{u}=\left[\begin{array}{cc}1& -3\\ 3& 5\\ -1& 7\end{array}\right]\left[\begin{array}{c}2\\ -1\end{array}\right]=\left[\begin{array}{c}1(2)+(-3)(-1)\\ 3(2)+5(-1)\\ -1(2)+7(-1)\end{array}\right]=\left[\begin{array}{c}5\\ 1\\ -9\end{array}\right]$

Interpretación: La transformación $T$ mapea vectores de ${\mathbb{R}}^2$ a ${\mathbb{R}}^3$.

---

3. Transformaciones Geométricas en ${\mathbb{R}}^2$

3.1 Reflexiones

Ejemplo 2

Reflexión a Través del Eje $x_1$

Transformación: Reflejar vectores a través del eje $x_1$ (eje horizontal).

Efecto geométrico: $\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\mapsto \left[\begin{array}{c}{x}_1\\ -x_2\end{array}\right]$

Matriz estándar: $A=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$

Verificación: $\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}{x}_1\\ -x_2\end{array}\right]$

Ejemplo 3

Reflexión a Través del Eje $x_2$

Matriz estándar: $A=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]$

Efecto: $\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\mapsto \left[\begin{array}{c}-x_1\\ x_2\end{array}\right]$

Ejemplo 4

Reflexión a Través de la Recta $x_2=x_1$

Matriz estándar: $A=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]$

Efecto: Intercambia las coordenadas, $\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\mapsto \left[\begin{array}{c}{x}_2\\ x_1\end{array}\right]$

3.2 Contracciones y Expansiones

Ejemplo 5 - Contracción/Expansión Horizontal

Sea $k>0$ un escalar. La transformación $T(\mathbf{x})=\left[\begin{array}{cc}k& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}k{x}_1\\ x_2\end{array}\right]$

• Si $0<k<1$: Contracción horizontal
• Si $k>1$: Expansión horizontal
• La coordenada vertical permanece sin cambio

3.3 Transformaciones de Traslación (Traslación)

Ejemplo 6 - Traslación (Trasladar por un Vector)

Sea $\mathbf{p}=\left[\begin{array}{c}1\\ 2\end{array}\right]$ un vector fijo.

La transformación $T(\mathbf{x})=\mathbf{x}+\mathbf{p}$ traslada cada vector por $\mathbf{p}$:

$T\left(\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\right)=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\left[\begin{array}{c}1\\ 2\end{array}\right]=\left[\begin{array}{c}{x}_1+1\\ x_2+2\end{array}\right]$

Importante: Esta transformación NO es una transformación matricial (no preserva el origen).

3.4 Proyecciones

Ejemplo 7

Proyección sobre el Eje $x_1$

Transformación: Proyectar vectores perpendicularmente sobre el eje $x_1$.

Matriz estándar: $A=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]$

Efecto: $\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\mapsto \left[\begin{array}{c}{x}_1\\ 0\end{array}\right]$

Interpretación geométrica: Colapsa el plano sobre el eje horizontal.

---

4. Transformaciones Lineales

4.1 Definición Formal

Definición - Transformación Lineal

Una transformación (o mapeo) $T:{\mathbb{R}}^n\to {\mathbb{R}}^m$ es lineal si:

(L1) Preserva la suma: $T(\mathbf{u}+\mathbf{v})=T(\mathbf{u})+T(\mathbf{v})$ para todos $\mathbf{u},\mathbf{v}$ en ${\mathbb{R}}^n$

(L2) Preserva la multiplicación escalar: $T(c\mathbf{u})=cT(\mathbf{u})$ para todo escalar $c$ y todo $\mathbf{u}$ en ${\mathbb{R}}^n$

4.2 Propiedades Derivadas

Teorema - Propiedades de Transformaciones Lineales

Si $T$ es una transformación lineal, entonces:

1. Mapea el origen al origen: $T(0)=0$

2. Preserva combinaciones lineales: $T(c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2+\cdots +c_p{\mathbf{v}}_p)=c_{1}T({\mathbf{v}}_1)+c_{2}T({\mathbf{v}}_2)+\cdots +c_{p}T({\mathbf{v}}_p)$

3. Preserva paralelismo: Si dos rectas son paralelas, sus imágenes también lo son (o son el mismo conjunto)

4.3 Demostración de $T(0)=0$

Prueba

Usando la propiedad (L2) con $c=0$: $T(0)=T(0\cdot \mathbf{u})=0\cdot T(\mathbf{u})=0$

4.4 Verificación de Linealidad

Ejemplo 8 - Verificar que una Transformación es Lineal

Sea $T:{\mathbb{R}}^2\to {\mathbb{R}}^2$ definida por $T\left(\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\right)=\left[\begin{array}{c}{x}_1+3x_2\\ 2x_1-x_2\end{array}\right]$

Verificar (L1): $T\left(\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]+\left[\begin{array}{c}{v}_1\\ v_2\end{array}\right]\right)=T\left(\left[\begin{array}{c}{u}_1+v_1\\ u_2+v_2\end{array}\right]\right)$ $=\left[\begin{array}{c}(u_1+v_1)+3(u_2+v_2)\\ 2(u_1+v_1)-(u_2+v_2)\end{array}\right]=\left[\begin{array}{c}{u}_1+3u_2\\ 2u_1-u_2\end{array}\right]+\left[\begin{array}{c}{v}_1+3v_2\\ 2v_1-v_2\end{array}\right]$ $=T\left(\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]\right)+T\left(\left[\begin{array}{c}{v}_1\\ v_2\end{array}\right]\right)$ ✓

Verificar (L2): $T\left(c\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]\right)=T\left(\left[\begin{array}{c}c{u}_1\\ c{u}_2\end{array}\right]\right)=\left[\begin{array}{c}c{u}_1+3c{u}_2\\ 2c{u}_1-c{u}_2\end{array}\right]$ $=c\left[\begin{array}{c}{u}_1+3u_2\\ 2u_1-u_2\end{array}\right]=cT\left(\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]\right)$ ✓

Conclusión: $T$ es lineal.

4.5 Ejemplo de Transformación NO Lineal

Ejemplo 9 - Transformación No Lineal

Sea $T\left(\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\right)=\left[\begin{array}{c}{x}_1+1\\ x_2\end{array}\right]$ (traslación)

Verificar si preserva el origen: $T\left(\left[\begin{array}{c}0\\ 0\end{array}\right]\right)=\left[\begin{array}{c}0+1\\ 0\end{array}\right]=\left[\begin{array}{c}1\\ 0\end{array}\right]\ne \left[\begin{array}{c}0\\ 0\end{array}\right]$

Como $T(0)\ne 0$, la transformación no es lineal.

---

5. Relación con Transformaciones Matriciales

5.1 Teorema Fundamental

Teorema 10 - Toda Transformación Matricial es Lineal

Si $A$ es una matriz $m\times n$, entonces la transformación $T(\mathbf{x})=A\mathbf{x}$ es una transformación lineal de ${\mathbb{R}}^n$ a ${\mathbb{R}}^m$.

Demostración: Se sigue directamente de las propiedades del producto matriz-vector (Teorema 5 de la Clase 7):

• $A(\mathbf{u}+\mathbf{v})=A\mathbf{u}+A\mathbf{v}$
• $A(c\mathbf{u})=c(A\mathbf{u})$

---

6. Rango de una Transformación

6.1 Definición

Definición - Rango

El rango de una transformación lineal $T:{\mathbb{R}}^n\to {\mathbb{R}}^m$ es el conjunto de todas las imágenes de vectores en ${\mathbb{R}}^n$:

$\text{Rango}(T)=\{T(\mathbf{x}):\mathbf{x}\in {\mathbb{R}}^n\}$

Para una transformación matricial $T(\mathbf{x})=A\mathbf{x}$, el rango de $T$ es el conjunto de todas las combinaciones lineales de las columnas de $A$.

6.2 Relación con Columnas

Observación Clave

Para $T(\mathbf{x})=A\mathbf{x}$ donde $A=[{\mathbf{a}}_1{\mathbf{a}}_2\cdots {\mathbf{a}}_n]$:

$\text{Rango}(T)=\text{Gen}\{{\mathbf{a}}_1,{\mathbf{a}}_2,\dots ,{\mathbf{a}}_n\}=\text{Col}(A)$

---

🚨 Errores Comunes

Error 1: Confundir transformación lineal con función lineal (de cálculo)

• Incorrecto: Pensar que $f(x)=2x+3$ es una transformación lineal
• Correcto: En álgebra lineal, una transformación lineal DEBE satisfacer $T(0)=0$. La función $f(x)=2x+3$ no lo hace.

Error 2: Asumir que todas las transformaciones geométricas son lineales

• Incorrecto: Las traslaciones son transformaciones lineales
• Correcto: Las traslaciones NO son lineales (no mapean el origen al origen)

Error 3: Verificar solo una propiedad

• Incorrecto: Solo verificar que $T(c\mathbf{u})=cT(\mathbf{u})$ y concluir que es lineal
• Correcto: Debe verificar AMBAS propiedades (L1) y (L2)

Error 4: Confundir dominio con codominio

• Incorrecto: Decir que el dominio es donde “aterrizan” los vectores
• Correcto: El dominio es de donde “salen” los vectores; el codominio es donde pueden “aterrizar”

---

📝 Ejercicios de Práctica

Ejercicios Básicos

Problemas Fundamentales

1. Calcular imágenes: Para $A=\left[\begin{array}{cc}2& -1\\ 1& 3\end{array}\right]$ y $T(\mathbf{x})=A\mathbf{x}$, calcule:

   a) $T\left(\left[\begin{array}{c}3\\ 1\end{array}\right]\right)$

   b) $T\left(\left[\begin{array}{c}-2\\ 4\end{array}\right]\right)$

2. Identificar transformaciones geométricas: Describa geométricamente cada transformación:

   a) $T(\mathbf{x})=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]\mathbf{x}$

   b) $T(\mathbf{x})=\left[\begin{array}{cc}2& 0\\ 0& 2\end{array}\right]\mathbf{x}$

   c) $T(\mathbf{x})=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right]\mathbf{x}$ (de ${\mathbb{R}}^3$ a ${\mathbb{R}}^2$)

3. Verificar linealidad: Determine si cada transformación es lineal:

   a) $T\left(\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\right)=\left[\begin{array}{c}{x}_1^2\\ x_2\end{array}\right]$

   b) $T\left(\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\right)=\left[\begin{array}{c}0\\ 0\end{array}\right]$

   c) $T\left(\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\right)=\left[\begin{array}{c}{x}_1-x_2\\ x_2-x_1\end{array}\right]$

Ejercicios Intermedios

Práctica de Conceptos

4. Construcción de matrices: Encuentre la matriz estándar para cada transformación geométrica en ${\mathbb{R}}^2$:

   a) Reflexión a través del origen b) Expansión por un factor de 3 en ambas direcciones c) Proyección sobre el eje $x_2$

5. Composición: Si $T(\mathbf{x})=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]\mathbf{x}$ y $S(\mathbf{x})=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]\mathbf{x}$, calcule $(S\circ T)\left(\left[\begin{array}{c}1\\ 0\end{array}\right]\right)$.

6. Análisis del rango: Para $T(\mathbf{x})=\left[\begin{array}{ccc}1& 2& 1\\ 2& 4& 2\end{array}\right]\mathbf{x}$, describa geométricamente el rango de $T$.

Ejercicios Avanzados

Problemas Conceptuales

7. Demostración: Demuestre que si $T$ es lineal, entonces $T(-\mathbf{v})=-T(\mathbf{v})$ para todo vector $\mathbf{v}$.

8. Contraejemplo: Proporcione un ejemplo de una transformación $T:{\mathbb{R}}^2\to {\mathbb{R}}^2$ que satisfaga $T(c\mathbf{u})=cT(\mathbf{u})$ pero NO sea lineal.

9. Ejercicio 19 (del libro): [Desarrollar según las indicaciones de la clase]

---

🎯 Conceptos Clave para Repasar

Resumen de Conceptos Fundamentales

1. Transformación: Regla que mapea vectores de un espacio a otro
2. Dominio, codominio, rango: Conjuntos involucrados en una transformación
3. Transformación matricial: $T(\mathbf{x})=A\mathbf{x}$
4. Linealidad: Preserva suma y multiplicación escalar
5. Propiedad del origen: $T(0)=0$ (necesaria para linealidad)
6. Toda transformación matricial es lineal
7. Transformaciones geométricas: Reflexiones, proyecciones, rotaciones, escalamientos
8. Rango: Conjunto de todas las imágenes posibles

---

✅ Checklist de Estudio

Lista de Verificación

• Entiendo qué es una transformación entre espacios vectoriales
• Puedo distinguir entre dominio, codominio y rango
• Sé calcular la imagen de un vector bajo una transformación matricial
• Comprendo las dos propiedades que definen una transformación lineal
• Puedo verificar si una transformación dada es lineal
• Reconozco transformaciones geométricas básicas (reflexión, proyección, etc.)
• Entiendo por qué las traslaciones NO son lineales
• Puedo describir el rango de una transformación matricial
• Relaciono las columnas de una matriz con el rango de la transformación

---

🔗 Conexiones con Otros Temas

Vínculos Conceptuales

Próxima clase:

• 14) Matriz de una Transformación Lineal: Matriz de una transformación lineal (representación completa)

Conceptos relacionados:

• Matriz-Estandar - Representación matricial de transformaciones lineales
• Kernel - Vectores que se mapean al origen
• Isomorfismo - Transformaciones lineales invertibles

---

📚 Referencias

Lectura Principal

• Lay, D. Álgebra Lineal y sus Aplicaciones. Sección 1.8, págs. 62-68

---

🏷️ Tags

algebra-lineal transformaciones-lineales transformacion-matricial linealidad reflexion proyeccion rango dominio codominio clase-13

---

Próxima Clase

En la Clase 14, profundizaremos en la matriz estándar de una transformación lineal y aprenderemos cómo cualquier transformación lineal de ${\mathbb{R}}^n$ a ${\mathbb{R}}^m$ puede representarse mediante multiplicación matricial.

---

Navegación

• ⬅️ Clase Anterior
• ➡️ Clase Siguiente