3) Calculo de limites y Leyes de los limites

Clase 03: Cálculo de Límites - Leyes de los Límites

📚 Introducción

Esta clase presenta las herramientas algebraicas fundamentales para calcular límites de manera sistemática. Las leyes de los límites nos permiten descomponer problemas complejos en partes más simples, facilitando el cálculo sin recurrir siempre a tablas numéricas o gráficas. Además, introducimos teoremas poderosos como el de compresión para casos más sofisticados.

Objetivos de la Clase

• Dominar las Leyes fundamentales de los límites
• Aplicar la propiedad de sustitución directa
• Comprender y utilizar el teorema de compresión
• Resolver límites mediante manipulación algebraica

---

1. Leyes Fundamentales de los Límites

1.1 Las 11 Leyes de los Leyes-de-Limites

Leyes de los Límites

Suponga $c$ una constante y que los límites ${\lim }_{x\to a}f(x)$ y ${\lim }_{x\to a}g(x)$ existen. Entonces:

$$\begin{array}{rl}1.& \underset{x\to a}{\lim }[f(x)+g(x)]=\underset{x\to a}{\lim }f(x)+\underset{x\to a}{\lim }g(x)\\ 2.& \underset{x\to a}{\lim }[f(x)-g(x)]=\underset{x\to a}{\lim }f(x)-\underset{x\to a}{\lim }g(x)\\ 3.& \underset{x\to a}{\lim }[cf(x)]=c\underset{x\to a}{\lim }f(x)\\ 4.& \underset{x\to a}{\lim }[f(x)g(x)]=\underset{x\to a}{\lim }f(x)\cdot \underset{x\to a}{\lim }g(x)\\ 5.& \underset{x\to a}{\lim }\frac{f(x)}{g(x)}=\frac{{\lim }_{x\to a}f(x)}{{\lim }_{x\to a}g(x)}\text{si }\underset{x\to a}{\lim }g(x)\ne 0\\ 6.& \underset{x\to a}{\lim }[f(x){]}^n={\left[\underset{x\to a}{\lim }f(x)\right]}^n\text{donde }n\text{ es entero positivo}\\ 7.& \underset{x\to a}{\lim }c=c\\ 8.& \underset{x\to a}{\lim }x=a\\ 9.& \underset{x\to a}{\lim }{x}^n=a^n\text{donde }n\text{ es entero positivo}\\ 10.& \underset{x\to a}{\lim }\sqrt[n]{x}=\sqrt[n]{a}\text{donde }n\text{ es entero positivo}\text{[Si }n\text{ es par, suponemos que }a>0\text{]}\\ 11.& \underset{x\to a}{\lim }\sqrt[n]{f(x)}=\sqrt[n]{\underset{x\to a}{\lim }f(x)}\text{donde }n\text{ es entero positivo}\text{[Si }n\text{ es par, suponemos que }\underset{x\to a}{\lim }f(x)>0\text{]}\end{array}$$

1.2 Interpretación Verbal de las Leyes

Ley	Nombre	Interpretación
1	Ley de la suma	El límite de una suma es la suma de los límites
2	Ley de la diferencia	El límite de una diferencia es la diferencia de los límites
3	Ley del múltiplo constante	El límite de una constante por una función es la constante por el límite
4	Ley del producto	El límite de un producto es el producto de los límites
5	Ley del cociente	El límite de un cociente es el cociente de los límites (si denominador ≠ 0)
6	Ley de la potencia	El límite de una potencia es la potencia del límite
7	Ley de la constante	El límite de una constante es la constante misma
8	Ley de la identidad	El límite de la variable es el valor al que se aproxima
9	Ley de la potencia de x	El límite de $x^n$ es $a^n$
10-11	Ley de la raíz	El límite de una raíz es la raíz del límite

Observación

Estas leyes solo se aplican cuando los límites involucrados existen. Si algún límite no existe, no podemos aplicar directamente estas reglas.

---

2. Propiedades Especiales

2.1 Propiedad de Sustitución Directa

Propiedad de Sustitución Directa

Si $f$ es una función polinomial o una función racional y $a$ está en el dominio de $f$, entonces: ${\lim }_{x\to a}f(x)=f(a)$

Implicación Práctica

Para funciones continuas en un punto, calcular el límite es tan simple como evaluar la función en ese punto.

2.2 Propiedad de Funciones Equivalentes

Funciones Equivalentes

Si $f(x)=g(x)$ cuando $x\ne a$, entonces: ${\lim }_{x\to a}f(x)={\lim }_{x\to a}g(x)$ siempre que el límite exista.

Importante

El valor de las funciones en el punto $a$ no afecta el límite. Solo importa el comportamiento cerca de $a$.

---

3. Teoremas Fundamentales

3.1 Teorema de Límites Laterales

Teorema - Existencia del Límite \lim_{x \to a} f(x) = L \quad \text{si y solo si} \quad \lim_{x \to a^-} f(x) = L = \lim_{x \to a^+} f(x)

3.2 Teorema de Comparación

Teorema de Comparación

Si $f(x)\le g(x)$ cuando $x$ tiende a $a$ (excepto posiblemente en $x=a$) y los límites de $f$ y $g$ existen cuando $x$ tiende a $a$, entonces: ${\lim }_{x\to a}f(x)\le {\lim }_{x\to a}g(x)$

3.3 Teorema de Compresión (Sandwich)

Teorema de Compresión

Si $f(x)\le g(x)\le h(x)$ cuando $x$ tiende a $a$ (excepto posiblemente en $a$) y ${\lim }_{x\to a}f(x)={\lim }_{x\to a}h(x)=L$ entonces: ${\lim }_{x\to a}g(x)=L$

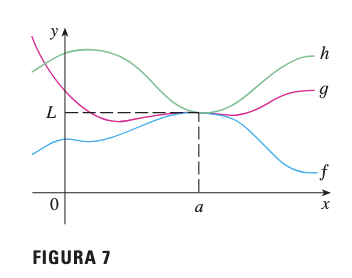
Interpretación Geométrica

Si $g(x)$ está “comprimida” entre $f(x)$ y $h(x)$ cerca de $a$, y ambas funciones extremas tienen el mismo límite $L$, entonces $g$ es forzada a tener el mismo límite.

---

4. Ejemplos Resueltos

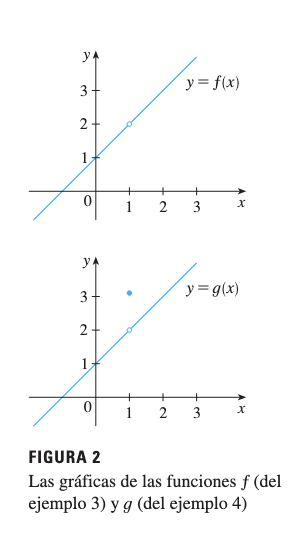
4.1 Ejemplo: Función Definida por Partes

Problema: Encuentre $\underset{x\to 1}{\lim }g(x)$ donde: $g(x)=\{\begin{array}{ll}x+1& \text{si }x\ne 1\\ \pi & \text{si }x=1\end{array}$

Solución

• El valor $g(1)=\pi$ no afecta el límite
• Para $x\ne 1$: $g(x)=x+1$
• Por lo tanto: ${\lim }_{x\to 1}g(x)={\lim }_{x\to 1}(x+1)=2$

4.2 Ejemplo: Simplificación Algebraica

Problema: Evalúe $\underset{h\to 0}{\lim }\frac{(3+h{)}^2-9}{h}$

Solución Paso a Paso

1. Expandir el numerador: $(3+h{)}^2-9=9+6h+h^2-9=6h+h^2$

2. Simplificar la fracción: $\frac{6h+h^2}{h}=\frac{h(6+h)}{h}=6+h(h\ne 0)$

3. Aplicar el límite: ${\lim }_{h\to 0}(6+h)=6$

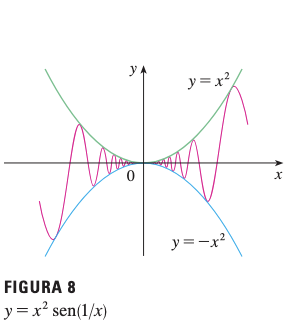
4.3 Ejemplo: Teorema de Compresión

Problema: Demuestre que $\underset{x\to 0}{\lim }{x}^2\sin \frac{1}{x}=0$

Solución usando Teorema de Compresión

Paso 1: Observar que no podemos usar la ley del producto directamente:

• ${\lim }_{x\to 0}\sin (1/x)$ no existe

Paso 2: Usar la acotación del seno: $-1\le \sin \frac{1}{x}\le 1$

Paso 3: Multiplicar por $x^2\ge 0$: $-x^2\le x^2\sin \frac{1}{x}\le x^2$

Paso 4: Aplicar el teorema de compresión:

• ${\lim }_{x\to 0}(-x^2)=0$
• ${\lim }_{x\to 0}{x}^2=0$
• Por lo tanto: ${\lim }_{x\to 0}{x}^2\sin \frac{1}{x}=0$

---

5. Estrategias de Cálculo

Estrategia 1: Sustitución Directa

1. Verificar si la función es continua en el punto
2. Si lo es, evaluar directamente: ${\lim }_{x\to a}f(x)=f(a)$
3. Aplicable a polinomios y funciones racionales (donde denominador ≠ 0)

Estrategia 2: Simplificación Algebraica

1. Factorizar numerador y denominador
2. Cancelar factores comunes (válido para $x\ne a$)
3. Aplicar el límite a la expresión simplificada
4. Útil para formas indeterminadas $\frac{0}{0}$

Estrategia 3: Aplicación de Leyes

1. Descomponer la función en partes más simples
2. Aplicar las leyes apropiadas
3. Calcular límites parciales
4. Combinar resultados

Estrategia 4: Teorema de Compresión

1. Identificar funciones que acoten superior e inferiormente
2. Verificar que ambas cotas tengan el mismo límite
3. Concluir que la función intermedia tiene ese límite
4. Útil para funciones oscilantes acotadas

---

6. Casos Especiales y Precauciones

6.1 Cuándo NO Aplicar las Leyes

Precaución con Límites No Existentes

No podemos aplicar las leyes si algún límite involucrado no existe:

• Incorrecto: ${\lim }_{x\to 0}x\cdot \sin (1/x)={\lim }_{x\to 0}x\cdot {\lim }_{x\to 0}\sin (1/x)$
• El segundo límite no existe

6.2 Formas Indeterminadas

Formas que Requieren Técnicas Especiales

• $\frac{0}{0}$: Intentar factorización o racionalización
• $\frac{\infty }{\infty }$: Puede requerir L’Hôpital (tema futuro)
• $0\cdot \infty$: Reescribir como cociente
• $\infty -\infty$: Manipulación algebraica cuidadosa

---

🎯 Conceptos Clave para Repasar

Resumen de Conceptos

1. Leyes de límites: 11 reglas fundamentales para operar con límites
2. Sustitución directa: Válida para funciones continuas
3. Simplificación algebraica: Clave para resolver formas indeterminadas
4. Teorema de compresión: Útil para funciones oscilantes acotadas
5. Funciones equivalentes: El valor en el punto no afecta el límite
6. Condiciones de aplicabilidad: Las leyes requieren que los límites existan

---

🚨 Errores Comunes

Error 1: Aplicar leyes cuando los límites no existen

• Incorrecto: Usar ley del producto si un factor no tiene límite
• Correcto: Verificar primero la existencia de todos los límites

Error 2: Confundir el valor de la función con el límite

• Incorrecto: Pensar que $g(1)=\pi$ implica ${\lim }_{x\to 1}g(x)=\pi$
• Correcto: El límite depende del comportamiento cerca del punto

Error 3: No simplificar antes de aplicar el límite

• Incorrecto: Concluir que ${\lim }_{h\to 0}\frac{h^2}{h}$ no existe
• Correcto: Simplificar primero a $h$ y luego calcular

Error 4: Olvidar restricciones en las leyes de raíces

• Incorrecto: Aplicar ley de raíz par con límite negativo
• Correcto: Verificar que el límite sea positivo para raíces pares

---

📝 Ejercicios Propuestos

Ejercicios de Práctica

1. Calcular ${\lim }_{x\to 2}\frac{x^3-8}{x-2}$ usando simplificación
2. Demostrar que ${\lim }_{x\to 0}x\cos (1/x)=0$ usando compresión
3. Evaluar ${\lim }_{x\to 3}\frac{\sqrt{x+1}-2}{x-3}$ mediante racionalización
4. Encontrar ${\lim }_{x\to 1}\frac{x^n-1}{x-1}$ para $n$ entero positivo

---

📚 Referencias

Lectura Principal

• Sección sobre Leyes de los Límites
• Teorema de Compresión y aplicaciones

Sugerencia de Estudio

Dominar las leyes de los límites es fundamental para todo el cálculo posterior. Practique identificando qué ley aplicar en cada situación y verificando siempre las condiciones de aplicabilidad.

---

✅ Checklist de Estudio

Lista de Verificación

• Puedo enunciar las 11 leyes de los límites
• Sé cuándo puedo usar sustitución directa
• Entiendo cuándo dos funciones tienen el mismo límite
• Puedo aplicar el teorema de compresión
• Reconozco cuándo NO puedo aplicar las leyes
• Sé simplificar algebraicamente antes de calcular límites
• Comprendo la diferencia entre el valor de una función y su límite
• Puedo identificar formas indeterminadas

---

🏷️ Tags

calculo limites leyes-de-limites teorema-de-compresion sustitucion-directa simplificacion-algebraica formas-indeterminadas clase-03 clase