4) Definicion precisa de limites

Clase 04: Definición Precisa de Límites

📚 Introducción

Esta clase presenta la definición formal y rigurosa del concepto de límite, proporcionando las herramientas matemáticas necesarias para demostrar con precisión cuándo una función se aproxima a un valor específico. Pasamos de la comprensión intuitiva a la formulación epsilon-delta (ε-δ), fundamental para el desarrollo riguroso del cálculo.

Objetivos de la Clase

• Comprender la relación entre la representación gráfica y formal (ε y δ) del concepto de límite
• Dominar la definición precisa de límite ${\lim }_{x\to a}f(x)=L$
• Comprender la relación entre la representación gráfica y formal (M y δ) del concepto de límite infinito
• Aplicar las definiciones para demostrar límites específicos

---

1. Definición Precisa de Límite

1.1 Definición Formal ε-δ

Definición - Límite de una Función

Sea $f$ una función definida sobre algún intervalo abierto que contiene el número $a$, excepto posiblemente en $a$ misma. Entonces, decimos que el límite de f(x) cuando x tiende a a es L, y lo expresamos como

${\lim }_{x\to a}f(x)=L$

si para cada número $\epsilon >0$ existe un número $\delta >0$ tal que

$\text{si }0<|x-a|<\delta \text{ entonces }|f(x)-L|<\epsilon$

1.2 Interpretación de la Definición

La definición establece que:

• Para cualquier tolerancia $\epsilon$ en el valor de la función (por pequeña que sea)
• Podemos encontrar una distancia $\delta$ desde $a$
• Tal que si $x$ está dentro de esa distancia de $a$ (pero $x\ne a$)
• Entonces $f(x)$ estará dentro de la tolerancia $\epsilon$ de $L$

Interpretación Intuitiva

Podemos hacer que $f(x)$ esté tan cerca de $L$ como queramos, tomando $x$ suficientemente cerca de $a$.

1.3 Representación Gráfica

La figura muestra cómo, dado un $\epsilon >0$, existe un $\delta >0$ tal que cuando $x$ está en el intervalo $(a-\delta ,a+\delta )$ con $x\ne a$, entonces $f(x)$ está en el intervalo $(L-\epsilon ,L+\epsilon )$.

---

2. Estrategia para Demostrar Límites

2.1 Proceso de Demostración

Para demostrar que ${\lim }_{x\to a}f(x)=L$ usando la definición ε-δ:

Método General

1. Análisis preliminar: Intuir la relación entre $\epsilon$ y $\delta$
   • Partir de $|f(x)-L|<\epsilon$
   • Manipular algebraicamente hasta obtener una expresión con $|x-a|$
   • Identificar cómo debe ser $\delta$ en términos de $\epsilon$
2. Demostración formal:
   • Dado $\epsilon >0$, escoger $\delta$ según el análisis preliminar
   • Verificar que si $0<|x-a|<\delta$, entonces $|f(x)-L|<\epsilon$
   • Concluir que por la definición de límite, ${\lim }_{x\to a}f(x)=L$

2.2 Ejemplo 1: Función Lineal

Demostrar que ${\lim }_{x\to 3}(4x-5)=7$

Solución

Análisis preliminar:

• Queremos que $|(4x-5)-7|<\epsilon$
• Simplificando: $|4x-12|=4|x-3|<\epsilon$
• Por lo tanto: $|x-3|<\epsilon /4$
• Esto sugiere elegir $\delta =\epsilon /4$

Demostración:

• Dado $\epsilon >0$, sea $\delta =\epsilon /4$
• Si $0<|x-3|<\delta$, entonces: $|(4x-5)-7|=|4x-12|=4|x-3|<4\delta =4\cdot \frac{\epsilon }{4}=\epsilon$
• Por lo tanto, ${\lim }_{x\to 3}(4x-5)=7$

---

3. Límites Laterales - Definición Precisa

3.1 Límite por la Izquierda

Definición - Límite por la Izquierda \Large\lim_{x \to a^-} f(x) = L

si para todo $\epsilon >0$ existe un número $\delta >0$ tal que:

$\text{si }a-\delta <x<a\text{ entonces }|f(x)-L|<\epsilon$

3.2 Límite por la Derecha

Definición - Límite por la Derecha \Large\lim_{x \to a^+} f(x) = L

si para todo $\epsilon >0$ existe un número $\delta >0$ tal que:

$\text{si }a<x<a+\delta \text{ entonces }|f(x)-L|<\epsilon$

3.3 Ejemplo 2: Límite Lateral

Demostrar que ${\lim }_{x\to 0^{+}}\sqrt{x}=0$

Solución

Análisis preliminar:

• Queremos que $|\sqrt{x}-0|<\epsilon$, es decir, $\sqrt{x}<\epsilon$
• Elevando al cuadrado: $x<{\epsilon }^2$
• Esto sugiere elegir $\delta ={\epsilon }^2$

Demostración:

• Dado $\epsilon >0$, sea $\delta ={\epsilon }^2$
• Si $0<x<\delta$, entonces: $\sqrt{x}<\sqrt{\delta }=\sqrt{{\epsilon }^2}=\epsilon$
• Por lo tanto, ${\lim }_{x\to 0^{+}}\sqrt{x}=0$

---

4. Límites Infinitos - Definición Precisa

4.1 Límite Infinito Positivo

Definición - Límite Infinito Positivo

Sea $f$ una función definida sobre algún intervalo abierto que contiene al número $a$, excepto posiblemente en $a$ misma. Entonces

${\lim }_{x\to a}f(x)=\infty$

significa que para todo número positivo $M$ existe un número positivo $\delta$ tal que

$\text{si }0<|x-a|<\delta \text{ entonces }f(x)>M$

Esto dice que los valores de $f(x)$ pueden hacerse arbitrariamente grandes (más grandes que cualquier número $M$ dado), tomando $x$ suficientemente cercano a $a$ (dentro de una distancia $\delta$, donde $\delta$ depende de $M$, pero con $x\ne a$). (Ver figura 10)

4.2 Límite Infinito Negativo

Definición - Límite Infinito Negativo \Large\lim_{x \to a} f(x) = -\infty

significa que para todo número negativo $N$ existe un número positivo $\delta$ tal que

$\text{si }0<|x-a|<\delta \text{ entonces }f(x)<N$

4.3 Interpretación Gráfica

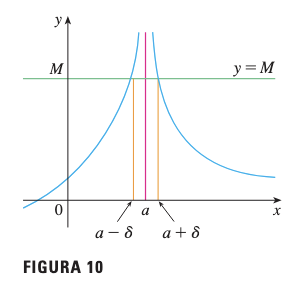
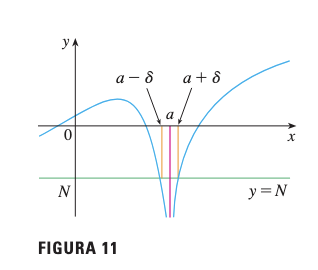
4.4 Ejemplo 3: Límite Infinito

Demostrar que ${\lim }_{x\to 0}\frac{1}{x^2}=\infty$

Solución

Análisis preliminar:

• Queremos que $\frac{1}{x^2}>M$
• Esto equivale a $x^2<\frac{1}{M}$, o bien $|x|<\frac{1}{\sqrt{M}}$
• Esto sugiere elegir $\delta =\frac{1}{\sqrt{M}}$

Demostración:

• Sea $M>0$ un número positivo dado
• Sea $\delta =\frac{1}{\sqrt{M}}$
• Si $0<|x|<\delta$, entonces: $x^2<{\delta }^2=\frac{1}{M}$ Por lo tanto: $\frac{1}{x^2}>M$
• Esto muestra que ${\lim }_{x\to 0}\frac{1}{x^2}=\infty$

---

5. Diferencias Clave entre Límites

5.1 Límite Existe vs No Existe

Recordatorio Fundamental

• ${\lim }_{x\to a}f(x)=L$ → El límite existe (L es un número real)
• ${\lim }_{x\to a}f(x)=\pm \infty$ → El límite NO existe (infinito no es un número real)

En el segundo caso, usamos la notación para describir la forma particular en que el límite no existe: la función crece o decrece sin cota.

5.2 Resumen de Definiciones

Tipo de Límite	Condición	Conclusión
$\underset{x\to a}{\lim }f(x)=L$	Si $0<\Vert x-a\Vert <\delta$	entonces $\Vert f(x)-L\Vert <\epsilon$
$\underset{x\to a^{-}}{\lim }f(x)=L$	Si $a-\delta <x<a$	entonces $\Vert f(x)-L\Vert <\epsilon$
$\underset{x\to a^{+}}{\lim }f(x)=L$	Si $a<x<a+\delta$	entonces $\Vert f(x)-L\Vert <\epsilon$
$\underset{x\to a}{\lim }f(x)=\infty$	Si $0<\Vert x-a\Vert <\delta$	entonces $f(x)>M$
$\underset{x\to a}{\lim }f(x)=-\infty$	Si $0<\Vert x-a\Vert <\delta$	entonces $f(x)<N$

---

🎯 Conceptos Clave para Repasar

Resumen de Conceptos

1. Definición ε-δ: Formalización rigurosa del concepto de límite
2. Proceso de demostración: Análisis preliminar + verificación formal
3. Relación ε-δ: Cómo la tolerancia en $y$ determina la proximidad en $x$
4. Límites laterales: Adaptación de la definición para aproximación unilateral
5. Límites infinitos: Uso de $M$ en lugar de $\epsilon$ para comportamiento no acotado
6. Interpretación gráfica: Visualización de las definiciones en el plano

---

🚨 Errores Comunes

Error 1: Confundir el orden de implicación

• Incorrecto: Dado $\delta$, encontrar $\epsilon$
• Correcto: Dado $\epsilon$, encontrar $\delta$

Error 2: No excluir el punto a

• Incorrecto: Usar $|x-a|<\delta$
• Correcto: Usar $0<|x-a|<\delta$ (excluye $x=a$)

Error 3: Elegir \delta dependiente de x

• Incorrecto: $\delta =x-a$
• Correcto: $\delta$ debe depender solo de $\epsilon$ (y de $a$), no de $x$

Error 4: Confundir límite infinito con límite existente

• Incorrecto: Decir que si ${\lim }_{x\to a}f(x)=\infty$, entonces el límite existe
• Correcto: El límite no existe; la notación describe cómo no existe

---

📚 Referencias

Lectura Principal

• Sección 2.4: Definición precisa de límite, págs. 108-116

Enlaces Relacionados

• Limite-de-una-funcion
• Limites-Infinitos

---

Sugerencia de Estudio

Enfatizar la diferencia entre ${\lim }_{x\to a}f(x)=L$ y ${\lim }_{x\to a}f(x)=\pm \infty$. En el primer caso, el límite existe por ser un número real. En el segundo caso, el límite NO existe, y esta es una notación conveniente para expresar que la función crece sin cota superior o decrece sin cota inferior. Es un buen momento para enfatizar la importancia de las definiciones matemáticas rigurosas.

---

✅ Checklist de Estudio

Lista de Verificación

• Comprendo la definición ε-δ y su interpretación geométrica
• Puedo realizar el análisis preliminar para encontrar δ en términos de ε
• Sé estructurar una demostración formal de límite
• Entiendo las modificaciones para límites laterales
• Comprendo la definición de límites infinitos con M y δ
• Puedo distinguir entre límite existe y límite no existe
• Reconozco la importancia de excluir el punto a en la definición
• Puedo interpretar gráficamente las definiciones formales

---

🏷️ Tags

calculo limites definicion-epsilon-delta limites-infinitos demostracion-formal limites-laterales definicion-precisa clase-04 clase