5) Limites Notables Cambio de Variables

Clase 05: Límites Notables y Cambio de Variables

📚 Introducción

Esta clase introduce límites fundamentales que aparecen frecuentemente en el cálculo y son esenciales para resolver problemas más complejos. Además, exploraremos la técnica del cambio de variable, una herramienta poderosa para transformar límites complicados en formas más manejables utilizando los límites notables.

Objetivos de la Clase

• Conocer los límites $\underset{x\to 0}{\lim }\sin (x)$, $\underset{x\to 0}{\lim }\cos (x)$, $\underset{x\to 0}{\lim }{e}^x$
• Dominar los límites notables: $\underset{x\to 0}{\lim }\frac{\sin (x)}{x}$, $\underset{x\to 0}{\lim }\frac{1-\cos (x)}{x^2}$, $\underset{x\to 0}{\lim }\frac{e^x-1}{x}$
• Calcular límites usando las leyes de los límites y límites conocidos
• Aplicar la técnica de cambio de variable para resolver límites

---

1. Límites Fundamentales

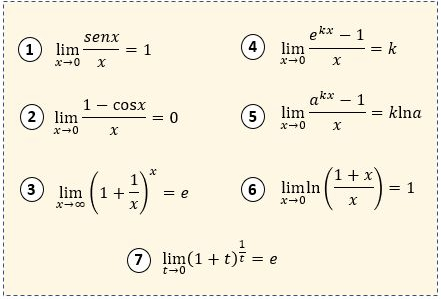
1.1 Límites Trigonométricos Básicos

Límites Trigonométricos Fundamentales

${\lim }_{x\to 0}\sin (x)=0\underset{x\to 0}{\lim }\frac{\sin (x)}{x}=1$ ${\lim }_{x\to 0}\cos (x)=1{\lim }_{x\to 0}\frac{e^x-1}{x}=1$

Estos límites se obtienen directamente de la continuidad de las funciones seno y coseno en $x=0$.

1.2 Límite Exponencial Básico

Definición del número e

$e$ es el número tal que:${\lim }_{h\to 0}\frac{e^h-1}{h}=1$

Límite Exponencial Fundamental

${\lim }_{x\to 0}{e}^x=1$

2. Límites Notables

2.1 Límite Notable del Seno

Límite Notable - Seno sobre x

${\lim }_{x\to 0}\frac{\sin (x)}{x}=1$

Este es uno de los límites más importantes en cálculo. Geométricamente, representa que para ángulos pequeños (en radianes), $\sin (x)\approx x$.

2.2 Límite Notable del Coseno

Límite Notable - Coseno

${\lim }_{x\to 0}\frac{1-\cos (x)}{x^2}=\frac{1}{2}$

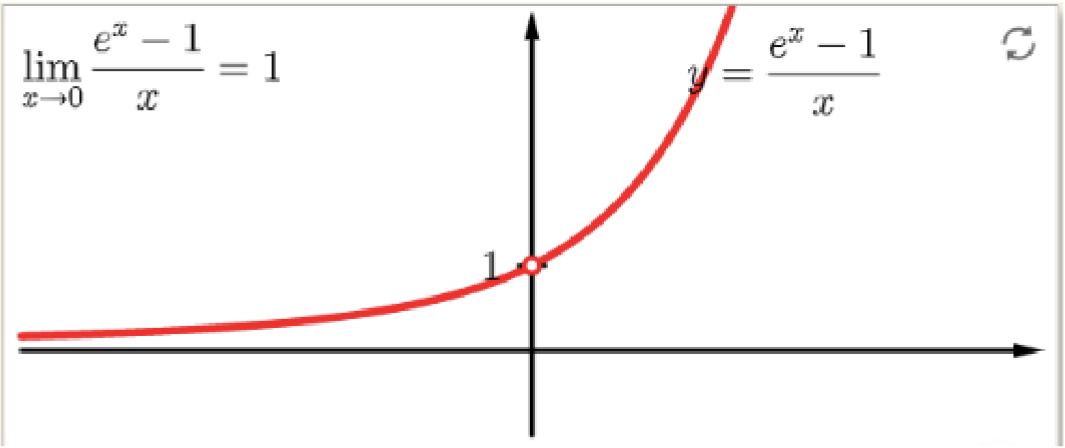
2.3 Límite Notable Exponencial

Límite Notable - Exponencial

${\lim }_{x\to 0}\frac{e^x-1}{x}=1$

2.4 Otros Límites Relacionados

Límite Derivado del Coseno

${\lim }_{x\to 0}\frac{\cos (x)-1}{x}=0$

Este límite se puede obtener usando la identidad $\cos (x)-1=-2{\sin }^2(x/2)$ y el límite notable del seno.

---

3. Técnica de Cambio de Variable

3.1 Principio del Cambio de Variable

Teorema - Cambio de Variable en Límites

Si ${\lim }_{x\to a}f(x)=b$ y ${\lim }_{y\to b}g(y)=L$ existe, entonces:

${\lim }_{x\to a}g(f(x))={\lim }_{y\to b}g(y)=L$

3.2 Estrategia de Aplicación

Método de Cambio de Variable

1. Identificar la estructura del límite que se asemeje a un límite notable
2. Definir una nueva variable $u$ que simplifique la expresión
3. Determinar hacia qué valor tiende $u$ cuando $x$ tiende a su valor
4. Reescribir el límite en términos de $u$
5. Aplicar el límite notable correspondiente

---

4. Ejemplos de Aplicación

4.1 Ejemplo 1: Límite con Múltiplo del Argumento

Calcular ${\lim }_{x\to 0}\frac{\sin (5x)}{x}$

Solución

Podemos reescribir: $\frac{\sin (5x)}{x}=\frac{\sin (5x)}{5x}\cdot 5$

Haciendo $u=5x$, cuando $x\to 0$, tenemos $u\to 0$

Por lo tanto: ${\lim }_{x\to 0}\frac{\sin (5x)}{x}=5\cdot {\lim }_{u\to 0}\frac{\sin (u)}{u}=5\cdot 1=5$

4.2 Ejemplo 2: Límite con Denominador Modificado

Calcular ${\lim }_{x\to 0}\frac{\sin (7x)}{4x}$

Solución

Reescribimos: $\frac{\sin (7x)}{4x}=\frac{7}{4}\cdot \frac{\sin (7x)}{7x}$

Con $u=7x$: ${\lim }_{x\to 0}\frac{\sin (7x)}{4x}=\frac{7}{4}\cdot {\lim }_{u\to 0}\frac{\sin (u)}{u}=\frac{7}{4}$

4.3 Ejemplo 3: Cambio de Variable con Raíces

Calcular ${\lim }_{y\to 1}\frac{\sqrt{y}-1}{\sqrt[3]{y}-1}$

Solución

Sea $u^6=y$, entonces cuando $y\to 1$, tenemos $u\to 1$

• $\sqrt{y}=u^3$
• $\sqrt[3]{y}=u^2$

El límite se transforma en: ${\lim }_{u\to 1}\frac{u^3-1}{u^2-1}={\lim }_{u\to 1}\frac{(u-1)(u^2+u+1)}{(u-1)(u+1)}={\lim }_{u\to 1}\frac{u^2+u+1}{u+1}=\frac{3}{2}$

4.4 Ejemplo 4: Límite con Traslación

Calcular ${\lim }_{x\to \pi }\frac{\sin (x)}{x-\pi }$

Solución

Sea $u=x-\pi$, entonces $x=u+\pi$ y cuando $x\to \pi$, tenemos $u\to 0$

Como $\sin (x)=\sin (u+\pi )=-\sin (u)$: ${\lim }_{x\to \pi }\frac{\sin (x)}{x-\pi }={\lim }_{u\to 0}\frac{-\sin (u)}{u}=-1$

---

5. Otros Límites Importantes

5.1 La Constante de Euler

Definición - Número e

$e={\lim }_{x\to \infty }{\left(1+\frac{1}{x}\right)}^x$

5.2 Ejercicios Propuestos

Ejercicios para Practicar

1. Calcular ${\lim }_{x\to 0}\frac{\sin (x)+x}{x\cos (x)}$
2. Calcular ${\lim }_{x\to 0}\frac{e^{2x}-1}{x}$
3. Calcular ${\lim }_{x\to \infty }{\left(1+\frac{1}{x}\right)}^{2x-1}$
4. Demostrar que ${\lim }_{x\to 0}\frac{1-\cos (x)}{x}=0$

---

6. Límites que No Existen

6.1 Ejemplos de Oscilación

Algunos límites no existen debido a la oscilación infinita de la función cerca del punto:

Límites Oscilantes

• ${\lim }_{x\to 0}\sin \left(\frac{1}{x}\right)$ no existe
• ${\lim }_{x\to 0}\cos \left(\frac{1}{x}\right)$ no existe

Estas funciones oscilan infinitamente entre -1 y 1 cuando $x\to 0$.

---

🎯 Conceptos Clave para Repasar

Resumen de Conceptos

1. Límites fundamentales: Valores básicos de seno, coseno y exponencial en 0
2. Límites notables: Tres límites esenciales que aparecen frecuentemente
3. Cambio de variable: Técnica para transformar límites complejos en notables
4. Constante e: Definición como límite fundamental
5. Aplicaciones: Uso combinado de leyes de límites y límites notables
6. Límites oscilantes: Casos donde el límite no existe por oscilación

---

🚨 Errores Comunes

Error 1: Aplicar límite notable incorrectamente

• Incorrecto: ${\lim }_{x\to 0}\frac{\sin (5x)}{x}=1$
• Correcto: ${\lim }_{x\to 0}\frac{\sin (5x)}{x}=5$

Error 2: No verificar el punto al que tiende la nueva variable

• Incorrecto: Asumir que la nueva variable siempre tiende a 0
• Correcto: Verificar hacia dónde tiende $u$ cuando $x$ tiende a su valor

Error 3: Confundir radianes con grados

• Incorrecto: Usar límites notables con ángulos en grados
• Correcto: Los límites notables solo son válidos con radianes

Error 4: No simplificar antes de aplicar el cambio

• Incorrecto: Hacer cambios de variable complicados innecesarios
• Correcto: Simplificar algebraicamente primero cuando sea posible

---

📚 Referencias

Lectura Principal

• Sección 3.1: Derivadas de funciones polinomiales y exponenciales, pág. 180
• Sección 3.2: Derivadas de funciones trigonométricas, págs. 192 y 196

Enlaces Relacionados

• Limites-Notables
• Cambio-de-Variable

---

Sugerencia de Estudio

Puede usar algún software (GeoGebra) para graficar las funciones y conjeturar los valores de los diferentes límites. Explicar que en ocasiones el cálculo del límite no es por simple manipulación algebraica de la fórmula que representa a la función, y se deben usar resultados (como el teorema de la compresión) para obtener su valor.

---

✅ Checklist de Estudio

Lista de Verificación

• Memorizo los tres límites notables fundamentales
• Puedo aplicar cambio de variable correctamente
• Verifico siempre hacia dónde tiende la nueva variable
• Reconozco cuándo usar cada límite notable
• Puedo combinar límites notables con las leyes de límites
• Entiendo por qué algunos límites oscilantes no existen
• Practico con ejercicios de diferentes tipos
• Uso radianes al trabajar con funciones trigonométricas

---

🏷️ Tags

calculo limites limites-notables cambio-de-variable seno coseno exponencial constante-e clase-05 clase