9) Limites al Infinito y Asintotas Horizontales

Clase 09: Límites al Infinito y Asíntotas Horizontales

📚 Introducción

Esta clase extiende nuestro estudio de límites hacia el comportamiento de funciones cuando la variable crece sin cota. Analizaremos qué sucede con los valores de una función cuando $x$ se hace arbitrariamente grande (positivo o negativo), introduciendo el concepto fundamental de asíntota horizontal y explorando casos donde las funciones crecen sin límite.

Objetivos de la Clase

• Comprender gráfica y numéricamente el concepto de límite al infinito ${\lim }_{x\to \infty }f(x)=L$
• Relacionar los límites al infinito con el concepto de Asintota-Horizontal
• Comprender gráfica y numéricamente el concepto de límite infinito en el infinito
• Determinar la existencia de límite al infinito
• Calcular límites al infinito
• Calcular límites infinitos en el infinito

---

1. Límites al Infinito

1.1 Definición para $x\to +\infty$

Definición - Límite cuando x tiende a infinito

Sea $f$ una función definida sobre algún intervalo $(a,\infty )$. Entonces: ${\lim }_{x\to \infty }f(x)=L$

Significa que los valores de $f(x)$ pueden aproximarse arbitrariamente a $L$ tanto como desee, eligiendo a $x$ suficientemente grande.

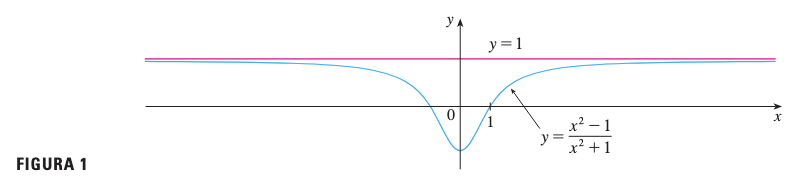
Interpretación Intuitiva

Podemos hacer que $f(x)$ esté tan cerca de $L$ como queramos, tomando $x$ suficientemente grande. La función se “estabiliza” alrededor del valor $L$ cuando nos movemos hacia la derecha en el eje $x$.

1.2 Definición para $x\to -\infty$

Definición - Límite cuando x tiende a menos infinito

Sea $f$ una función definida sobre algún intervalo $(-\infty ,a)$. Entonces: ${\lim }_{x\to -\infty }f(x)=L$

Significa que los valores de $f(x)$ pueden aproximarse arbitrariamente a $L$ tanto como desee, eligiendo a $x$ negativa y suficientemente grande en magnitud.

1.3 Ejemplo Fundamental

Problema: Calcule los siguientes límites:

1. ${\lim }_{x\to \infty }\frac{x^2-1}{x^2+1}$
2. ${\lim }_{x\to -\infty }\frac{x^2-1}{x^2+1}$

Solución

Para evaluar límites de funciones racionales cuando $x\to \pm \infty$, dividimos numerador y denominador por la mayor potencia de $x$ en el denominador:

$\frac{x^2-1}{x^2+1}=\frac{x^2/x^2-1/x^2}{x^2/x^2+1/x^2}=\frac{1-1/x^2}{1+1/x^2}$

Cuando $x\to \infty$: $\frac{1}{x^2}\to 0$, por lo tanto: ${\lim }_{x\to \infty }\frac{x^2-1}{x^2+1}=\frac{1-0}{1+0}=1$

El mismo análisis aplica para $x\to -\infty$: ${\lim }_{x\to -\infty }\frac{x^2-1}{x^2+1}=1$

---

2. Asíntotas Horizontales

2.1 Definición de Asintota-Horizontal

Definición - Asíntota Horizontal

La recta $y=L$ se llama asíntota horizontal de la curva $y=f(x)$ si ${\lim }_{x\to \infty }f(x)=L\text{oˊ}{\lim }_{x\to -\infty }f(x)=L$

Observación Clave

Una función puede tener:

• Ninguna asíntota horizontal
• Una asíntota horizontal (la misma cuando $x\to \infty$ y $x\to -\infty$)
• Dos asíntotas horizontales diferentes (una para cada dirección)
• Nunca puede tener más de dos asíntotas horizontales

2.2 Ejemplo: Función Arcotangente

Problema: Determine las asíntotas horizontales de $f(x)=\arctan (x)$

Solución

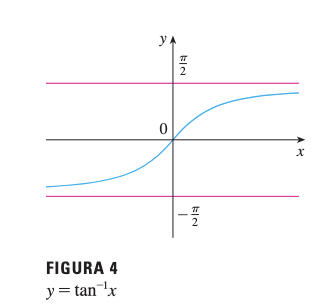
Recordando el comportamiento de la función arcotangente:

• ${\lim }_{x\to \infty }\arctan (x)=\frac{\pi }{2}$
• ${\lim }_{x\to -\infty }\arctan (x)=-\frac{\pi }{2}$

Por lo tanto, $f(x)=\arctan (x)$ tiene dos asíntotas horizontales:

• $y=\frac{\pi }{2}$ (cuando $x\to \infty$)
• $y=-\frac{\pi }{2}$ (cuando $x\to -\infty$)

---

3. Teorema Fundamental para Potencias

Teorema - Límite de Potencias Racionales

Si $r>0$ es un número racional, entonces: ${\lim }_{x\to \infty }\frac{1}{x^r}=0$

Si $r>0$ es un número racional tal que $x^r$ está definida para toda $x$, entonces: ${\lim }_{x\to -\infty }\frac{1}{x^r}=0$

Implicación Práctica

Este teorema es fundamental para calcular límites de funciones racionales:

• Términos como $\frac{1}{x}$, $\frac{1}{x^2}$, $\frac{1}{x^3}$ tienden a 0 cuando $x\to \pm \infty$
• Nos permite simplificar expresiones complejas dividiendo por potencias de $x$

---

4. Estrategia para Funciones Racionales

4.1 Método General

Estrategia para \frac{P(x)}{Q(x)} cuando x \to \pm\infty

Sea $\frac{a_n{x}^n+a_{n-1}{x}^{n-1}+...+a_0}{b_m{x}^m+b_{m-1}{x}^{m-1}+...+b_0}$ una función racional.

1. Dividir numerador y denominador por $x^m$ (mayor potencia del denominador)
2. Aplicar el teorema de límites de potencias
3. Analizar según los grados:
   • Si $n<m$: límite es 0
   • Si $n=m$: límite es $\frac{a_n}{b_m}$
   • Si $n>m$: límite es $\pm \infty$ (ver sección siguiente)

4.2 Ejemplo Completo

Problema: Encuentre las asíntotas horizontales y verticales de $f(x)=\frac{\sqrt{2x^2+1}}{3x-5}$

Solución Detallada

Asíntotas Verticales:

• El denominador se anula cuando $3x-5=0$, es decir, $x=\frac{5}{3}$
• Por lo tanto, $x=\frac{5}{3}$ es asíntota vertical

Asíntotas Horizontales: Para $x\to \infty$ (donde $x>0$): $\frac{\sqrt{2x^2+1}}{3x-5}=\frac{\sqrt{2x^2+1}/x}{(3x-5)/x}=\frac{\sqrt{2+1/x^2}}{3-5/x}$

Como $x\to \infty$: ${\lim }_{x\to \infty }\frac{\sqrt{2+0}}{3-0}=\frac{\sqrt{2}}{3}$

Para $x\to -\infty$ (donde $x<0$, así que $\sqrt{x^2}=|x|=-x$): $\frac{\sqrt{2x^2+1}}{3x-5}=\frac{-\sqrt{2+1/x^2}}{3-5/x}$

Como $x\to -\infty$: ${\lim }_{x\to -\infty }\frac{-\sqrt{2}}{3}=-\frac{\sqrt{2}}{3}$

Conclusión: Dos asíntotas horizontales: $y=\pm \frac{\sqrt{2}}{3}$

---

5. Límites Infinitos en el Infinito

5.1 Definición

Definición - Límite Infinito en el Infinito

La notación ${\lim }_{x\to \infty }f(x)=\infty$

se utiliza para indicar que los valores de $f(x)$ se hacen más grandes cuando $x$ se hace muy grande.

Un significado similar está asociado con los siguientes símbolos:

• ${\lim }_{x\to -\infty }f(x)=\infty$
• ${\lim }_{x\to \infty }f(x)=-\infty$
• ${\lim }_{x\to -\infty }f(x)=-\infty$

Importante sobre la Notación

Cuando escribimos ${\lim }_{x\to \infty }f(x)=\infty$:

• NO significa que el límite existe
• Describe que la función crece sin cota
• Es una forma especial de decir que el límite no existe

5.2 Ejemplos de Comportamiento Polinomial

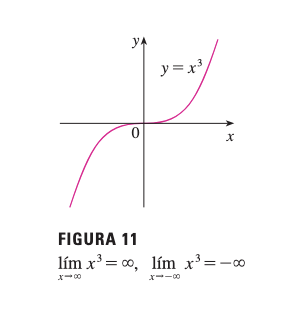
Problema: Determine ${\lim }_{x\to \infty }{x}^3$ y ${\lim }_{x\to -\infty }{x}^3$

Análisis

• Cuando $x\to \infty$: $x^3$ crece sin límite, así que ${\lim }_{x\to \infty }{x}^3=\infty$
• Cuando $x\to -\infty$: $x^3$ decrece sin límite, así que ${\lim }_{x\to -\infty }{x}^3=-\infty$

Observación: El comportamiento en el infinito de un polinomio está determinado por su término de mayor grado.

---

6. Funciones Especiales

6.1 Función Exponencial

Límites de la Función Exponencial

Para la función exponencial $f(x)=e^x$:

• ${\lim }_{x\to \infty }{e}^x=\infty$
• ${\lim }_{x\to -\infty }{e}^x=0$

Para $f(x)=e^{1/x}$:

• ${\lim }_{x\to 0^{-}}{e}^{1/x}=0$
• ${\lim }_{x\to 0^{+}}{e}^{1/x}=\infty$
• ${\lim }_{x\to \infty }{e}^{1/x}=1$

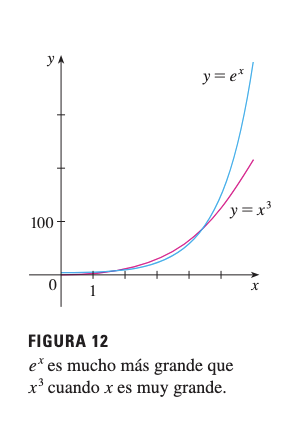
Observación

La función exponencial $e^x$ crece más rápidamente que cualquier polinomio cuando $x\to \infty$

6.2 Funciones con Radicales

Problema: Determine ${\lim }_{x\to \infty }(\sqrt{x^2+1}-x)$

Solución usando Racionalización

Multiplicamos y dividimos por el conjugado:

$\sqrt{x^2+1}-x=\frac{(\sqrt{x^2+1}-x)(\sqrt{x^2+1}+x)}{\sqrt{x^2+1}+x}$

$=\frac{x^2+1-x^2}{\sqrt{x^2+1}+x}=\frac{1}{\sqrt{x^2+1}+x}$

Como $x\to \infty$: el denominador $\to \infty$, por lo tanto: ${\lim }_{x\to \infty }(\sqrt{x^2+1}-x)=0$

Error Común

Incorrecto: ${\lim }_{x\to \infty }(\sqrt{x^2+1}-x)=\infty -\infty =0$

Correcto: La forma $\infty -\infty$ es indeterminada y requiere manipulación algebraica

---

7. Ejercicios Resueltos

7.1 Ejercicio: Límite Racional

Calcule ${\lim }_{x\to \infty }\frac{3x^2-x-2}{5x^2+4x+1}$

Solución

Dividimos por $x^2$: $\frac{3x^2-x-2}{5x^2+4x+1}=\frac{3-1/x-2/x^2}{5+4/x+1/x^2}$

Aplicando límites: ${\lim }_{x\to \infty }\frac{3-0-0}{5+0+0}=\frac{3}{5}$

7.2 Ejercicio: Comportamiento Mixto

Determine ${\lim }_{x\to 2^{+}}\arctan \left(\frac{1}{x-2}\right)$

Solución Cuando x \to 2^+:

• $x-2\to 0^{+}$
• $\frac{1}{x-2}\to +\infty$
• $\arctan (t)\to \frac{\pi }{2}$ cuando $t\to +\infty$

Por lo tanto: ${\lim }_{x\to 2^{+}}\arctan \left(\frac{1}{x-2}\right)=\frac{\pi }{2}$

---

🎯 Conceptos Clave para Repasar

Resumen de Conceptos

1. Límite al infinito: Comportamiento cuando $x$ crece sin cota
2. Asíntota horizontal: Recta a la que se aproxima la función
3. Estrategia para racionales: Dividir por mayor potencia
4. Límites infinitos en infinito: Crecimiento sin cota
5. Formas indeterminadas: $\infty -\infty$ requiere manipulación
6. Comportamiento de especiales: Exponencial, logaritmo, trigonométricas

---

🚨 Errores Comunes

Error 1: No identificar la mayor potencia correctamente

• Incorrecto: En $\frac{\sqrt{x^2+1}}{x}$, dividir por $x^2$
• Correcto: Dividir por $x$ (equivalente a $x^1$)

Error 2: Olvidar el signo en raíces cuando x < 0

• Incorrecto: $\sqrt{x^2}=x$ siempre
• Correcto: $\sqrt{x^2}=|x|$, que es $-x$ cuando $x<0$

Error 3: Operar con infinito como número

• Incorrecto: $\infty -\infty =0$
• Correcto: $\infty -\infty$ es indeterminado

Error 4: Asumir que toda función tiene asíntota horizontal

• Incorrecto: Toda función debe tener al menos una
• Correcto: Funciones como $e^x$ o $x^2$ no tienen asíntotas horizontales

---

📝 Ejercicios Propuestos

Ejercicios de Práctica

1. Determine ${\lim }_{x\to \infty }\frac{x^2+x}{3-x}$
2. Encuentre todas las asíntotas de $f(x)=\frac{2x^2+1}{3x-5}$
3. Calcule ${\lim }_{x\to \infty }(\sqrt{x^2+1}-x)$
4. Determine ${\lim }_{x\to 2^{+}}\arctan \left(\frac{1}{x-2}\right)$
5. Evalúe ${\lim }_{x\to -\infty }{e}^x$ y ${\lim }_{x\to 0^{-}}{e}^{1/x}$
6. Trace la gráfica de $y=(x-2{)}^4(x+1{)}^3(x-1)$ encontrando sus límites en $\pm \infty$

---

📚 Referencias

Lectura Principal

• Sección 2.6: Límites al infinito, asíntotas horizontales, págs. 130-137

Sugerencias de Estudio

Indicaciones Importantes

• Enfatizar que la existencia del límite al infinito se explica como la aproximación de la gráfica de la función a una recta horizontal en la medida que el valor de la variable crece ($x\to \infty$ o $x\to -\infty$)
• Explicitar un límite al infinito que el límite existe
• Explicitar en límite infinito en el infinito que el límite NO existe
• Mencionar que para funciones racionales: $\frac{P(x)}{Q(x)}\approx \frac{a_n{x}^n}{b_m{x}^m}=\frac{a_n}{b_m}{x}^{n-m}\text{cuando }x\to \pm \infty$ siendo $n$ y $m$ los grados de $P$ y $Q$ respectivamente

---

✅ Checklist de Estudio

Lista de Verificación

• Puedo calcular límites cuando $x\to \pm \infty$
• Identifico asíntotas horizontales algebraicamente
• Aplico la estrategia de división por mayor potencia
• Distingo entre límite existe (finito) y no existe (infinito)
• Manejo correctamente el signo de raíces cuando $x<0$
• Reconozco formas indeterminadas y sé resolverlas
• Comprendo el comportamiento de funciones especiales
• Puedo analizar funciones mixtas (racionales con radicales)

---

🏷️ Tags

calculo limites limites-infinito asintotas-horizontales funciones-racionales comportamiento-asintotico limites-infinitos-infinito clase-09 clase