3) Ángulos entre Vectores y Ecuaciones de Rectas

Clase 03: Ángulos entre Vectores y Ecuaciones de Rectas

📚 Introducción

Esta clase conecta los conceptos de producto punto desarrollados en la clase anterior con aplicaciones geométricas fundamentales: el cálculo de ángulos entre vectores y la descripción de rectas en el espacio. Estas herramientas nos permitirán abordar problemas geométricos usando técnicas algebraicas.

Objetivos de la Clase

• Calcular ángulos entre vectores usando el producto punto
• Identificar vectores ortogonales y sus propiedades
• Establecer ecuaciones de rectas en ${\mathbb{R}}^2$ y ${\mathbb{R}}^3$
• Dominar las formas vectorial, paramétrica y cartesiana de rectas
• Generalizar conceptos a ${\mathbb{R}}^n$

---

1. Ángulos entre Vectores

1.1 Fórmula del Coseno para Vectores

Teorema - Fórmula del Coseno

Para vectores no nulos $\mathbf{u}$ y $\mathbf{v}$ en ${\mathbb{R}}^n$, el ángulo $\theta$ entre ellos satisface:

$\cos \theta =\frac{\mathbf{u}\cdot \mathbf{v}}{|\mathbf{u}||\mathbf{v}|}$

donde $0\le \theta \le 180°$

Interpretación Geométrica

Esta fórmula generaliza la ley de cosenos del triángulo a espacios de cualquier dimensión, permitiendo calcular ángulos usando únicamente operaciones algebraicas.

1.2 Justificación de la Fórmula

La fórmula proviene de la desigualdad de Cauchy-Schwarz: $|\mathbf{u}\cdot \mathbf{v}|\le |\mathbf{u}||\mathbf{v}|$

Esto garantiza que $-1\le \frac{\mathbf{u}\cdot \mathbf{v}}{|\mathbf{u}||\mathbf{v}|}\le 1$, asegurando que el coseno esté bien definido.

1.3 Casos Especiales

Valor de $\cos \theta$	Ángulo $\theta$	Significado Geométrico
$\cos \theta =1$	$\theta =0°$	Vectores paralelos (misma dirección)
$\cos \theta =0$	$\theta =90°$	Vectores ortogonales
$\cos \theta =-1$	$\theta =180°$	Vectores paralelos (dirección opuesta)

1.4 Ejemplos de Cálculo de Ángulos

Ejemplo 1 - Ángulo entre Vectores en \mathbb{R}^3

Problema: Calcule el ángulo entre $\mathbf{u}=[2,-1,2]$ y $\mathbf{v}=[1,1,1]$

Solución:

1. $\mathbf{u}\cdot \mathbf{v}=2(1)+(-1)(1)+2(1)=2-1+2=3$
2. $|\mathbf{u}|=\sqrt{4+1+4}=3$
3. $|\mathbf{v}|=\sqrt{1+1+1}=\sqrt{3}$
4. $\cos \theta =\frac{3}{3\sqrt{3}}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$
5. $\theta =\arccos \left(\frac{\sqrt{3}}{3}\right)\approx 54.7°$

---

2. Vectores Ortogonales

2.1 Definición

Definición - Vectores Ortogonales

Los vectores $\mathbf{u}$ y $\mathbf{v}$ en ${\mathbb{R}}^n$ son ortogonales si:

$\mathbf{u}\cdot \mathbf{v}=0$

Se denota: $\mathbf{u}\perp \mathbf{v}$

2.2 Propiedades Importantes

Propiedades de la Ortogonalidad

1. Vector cero: El vector cero es ortogonal a cualquier vector
2. Teorema de Pitágoras: Si $\mathbf{u}\perp \mathbf{v}$, entonces: $|\mathbf{u}+\mathbf{v}{|}^2=|\mathbf{u}{|}^2+|\mathbf{v}{|}^2$
3. Descomposición ortogonal: Todo vector se puede descomponer en componentes ortogonales

Ejemplo 2 - Verificar Ortogonalidad

Problema: Determine si $\mathbf{u}=[3,-2,1]$ y $\mathbf{v}=[2,1,4]$ son ortogonales

Solución: $\mathbf{u}\cdot \mathbf{v}=3(2)+(-2)(1)+1(4)=6-2+4=8\ne 0$

Por tanto, los vectores no son ortogonales.

---

3. Ecuaciones de Rectas

3.1 Conceptos Fundamentales

Una recta en el espacio queda completamente determinada por:

• Un punto $P$ sobre la recta
• Un vector director $\mathbf{d}\ne 0$ paralelo a la recta

3.2 Forma Vectorial

Definición - Ecuación Vectorial de una Recta

La recta que pasa por el punto $P$ con vector de posición $\mathbf{p}$ y tiene vector director $\mathbf{d}$ se describe por:

$\mathbf{r}=\mathbf{p}+t\mathbf{d}$

donde $t\in \mathbb{R}$ es el parámetro y $\mathbf{r}$ es el vector de posición de cualquier punto en la recta.

Interpretación

• Cuando $t=0$: $\mathbf{r}=\mathbf{p}$ (punto inicial)
• Cuando $t>0$: nos movemos en dirección de $\mathbf{d}$
• Cuando $t<0$: nos movemos en dirección opuesta a $\mathbf{d}$

3.3 Forma Paramétrica

Definición - Ecuaciones Paramétricas

Si $\mathbf{p}=[x_0,y_0,z_0]$ y $\mathbf{d}=[a,b,c]$, entonces:

$\{\begin{array}{l}x=x_0+tay=y_0+tbz=z_0+tc\end{array}$

donde $t\in \mathbb{R}$ es el parámetro.

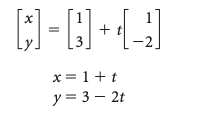
3.4 Forma Cartesiana (Simétrica)

Si todas las componentes del vector director son no nulas:

Definición - Ecuaciones Simétricas

$\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}$

Ejemplo 3 - Ecuación de una Recta

Problema: Encuentre las ecuaciones vectorial, paramétrica y simétrica de la recta que pasa por $P(1,-2,3)$ con vector director $\mathbf{d}=[2,1,-1]$

Solución:

Vectorial: $\mathbf{r}=[1,-2,3]+t[2,1,-1]$

Paramétrica: $\{\begin{array}{l}x=1+2ty=-2+tz=3-t\end{array}$

Simétrica: $\frac{x-1}{2}=\frac{y+2}{1}=\frac{z-3}{-1}$

---

4. Rectas en ${\mathbb{R}}^2$

4.1 Formas Especiales en el Plano

En ${\mathbb{R}}^2$, una recta puede expresarse como:

Formas de la Ecuación de una Recta en \mathbb{R}^2

Forma vectorial: $\mathbf{r}=\mathbf{p}+t\mathbf{d}$

Forma paramétrica: $\{\begin{array}{l}x=x_0+tay=y_0+tb\end{array}$

Forma simétrica: $\frac{x-x_0}{a}=\frac{y-y_0}{b}$ (si $a,b\ne 0$)

Forma punto-pendiente: $y-y_0=m(x-x_0)$ (si $b\ne 0$, $m=\frac{b}{a}$)

Forma general: $ax+by+c=0$

4.2 Vector Normal

Definición - Vector Normal

Para la recta $ax+by+c=0$ en ${\mathbb{R}}^2$, el vector $\mathbf{n}=[a,b]$ es normal (perpendicular) a la recta.

El vector director puede ser $\mathbf{d}=[-b,a]$ o $\mathbf{d}=[b,-a]$.

---

5. Relaciones entre Rectas

5.1 Paralelismo

Definición - Rectas Paralelas

Dos rectas con vectores directores ${\mathbf{d}}_1$ y ${\mathbf{d}}_2$ son paralelas si: ${\mathbf{d}}_1=k{\mathbf{d}}_2\text{ para alguˊn }k\ne 0$

5.2 Perpendicularidad

Definición - Rectas Perpendiculares

Dos rectas con vectores directores ${\mathbf{d}}_1$ y ${\mathbf{d}}_2$ son perpendiculares si: ${\mathbf{d}}_1\cdot {\mathbf{d}}_2=0$

---

6. Generalización a ${\mathbb{R}}^n$

6.1 Rectas en Espacios de Mayor Dimensión

Los conceptos se generalizan naturalmente:

Recta en \mathbb{R}^n

$\mathbf{r}=\mathbf{p}+t\mathbf{d}$

donde $\mathbf{p},\mathbf{d}\in {\mathbb{R}}^n$ y $\mathbf{d}\ne 0$

6.2 Hiperplanos

En ${\mathbb{R}}^n$, un hiperplano es un subespacio de dimensión $n-1$ que generaliza las rectas en ${\mathbb{R}}^2$ y los planos en ${\mathbb{R}}^3$.

---

🚨 Errores Comunes

Error 1: Confundir ángulo con coseno

• Incorrecto: Decir que el ángulo es $\frac{\mathbf{u}\cdot \mathbf{v}}{|\mathbf{u}||\mathbf{v}|}$
• Correcto: El coseno del ángulo es $\frac{\mathbf{u}\cdot \mathbf{v}}{|\mathbf{u}||\mathbf{v}|}$, el ángulo es $\arccos \left(\frac{\mathbf{u}\cdot \mathbf{v}}{|\mathbf{u}||\mathbf{v}|}\right)$

Error 2: Olvidar verificar que los vectores sean no nulos

• Incorrecto: Aplicar la fórmula del coseno con vectores cero
• Correcto: Verificar que $|\mathbf{u}|\ne 0$ y $|\mathbf{v}|\ne 0$

Error 3: Confundir vector director con vector normal

• Incorrecto: En ${\mathbb{R}}^2$, usar $[a,b]$ como vector director para la recta $ax+by+c=0$
• Correcto: $[a,b]$ es normal a la recta, el vector director es $[-b,a]$ o $[b,-a]$

---

Ejercicios Propuestos

Ejercicios de Práctica

1. Calcule el ángulo entre los vectores $[1,2,-1]$ y $[3,0,2]$
2. Determine si los vectores $[4,-2,6]$ y $[1,2,0]$ son ortogonales
3. Encuentre la ecuación vectorial de la recta que pasa por $(2,-1,3)$ y $(0,4,-2)$
4. Convierta a forma simétrica: $x=1+3t$, $y=-2+t$, $z=4-2t$
5. Determine si las rectas son paralelas, perpendiculares o ninguna:
   • $L_1$: $\mathbf{r}=[1,2,0]+t[2,-1,3]$
   • $L_2$: $\mathbf{r}=[0,1,2]+s[4,-2,6]$

---

🎯 Conceptos Clave para Repasar

Resumen de Conceptos

1. Ángulo entre vectores: Se calcula usando $\cos \theta =\frac{\mathbf{u}\cdot \mathbf{v}}{|\mathbf{u}||\mathbf{v}|}$
2. Ortogonalidad: Dos vectores son ortogonales si su producto punto es cero
3. Ecuación vectorial: $\mathbf{r}=\mathbf{p}+t\mathbf{d}$ describe una recta
4. Formas equivalentes: Vectorial, paramétrica y simétrica describen la misma recta
5. Relaciones: Paralelismo (vectores proporcionales) vs perpendicularidad (producto punto cero)

---

✅ Checklist de Estudio

Lista de Verificación

• Puedo calcular ángulos entre vectores en cualquier dimensión
• Sé identificar cuándo dos vectores son ortogonales
• Comprendo las diferentes formas de ecuaciones de rectas
• Puedo convertir entre formas vectorial, paramétrica y simétrica
• Identifico relaciones de paralelismo y perpendicularidad entre rectas
• Entiendo la generalización a espacios de mayor dimensión

---

📚 Referencias

Lectura Principal

• Poole, D. Álgebra lineal: Una introducción moderna. Sección 1.2, págs. 24-26; Sección 1.3, págs. 34-38

Temas Relacionados

• Producto-Punto - Operación fundamental
• Vectores-Ortogonales - Casos especiales importantes

---

🏷️ Tags

algebra-lineal angulos-vectores vectores-ortogonales ecuaciones-rectas forma-vectorial forma-parametrica forma-cartesiana paralelismo perpendicularidad clase-03 clase

---

Próxima Clase

En la Clase 04, estudiaremos planos en el espacio y su ecuación general, completando nuestro estudio de objetos geométricos básicos en ${\mathbb{R}}^3$.