2) Algebra de vectores y producto punto

Clase 02: Álgebra de Vectores y Producto Punto

📚 Introducción

Esta clase desarrolla las operaciones algebraicas fundamentales con vectores y presenta una de las herramientas más importantes del álgebra lineal: el producto punto. Esta operación nos permitirá calcular longitudes, distancias y ángulos, conectando conceptos geométricos con herramientas algebraicas.

Objetivos de la Clase

• Dominar las propiedades algebraicas de los vectores en ${\mathbb{R}}^n$
• Comprender el producto punto y sus aplicaciones
• Calcular longitudes y distancias usando vectores
• Determinar ángulos entre vectores
• Aplicar conceptos de vectores unitarios y normalización

---

1. Repaso: Operaciones Básicas con Vectores

1.1 Operaciones Fundamentales

Para vectores $\mathbf{u},\mathbf{v}\in {\mathbb{R}}^n$ y escalares $c,d\in \mathbb{R}$:

Operaciones Vectoriales Básicas

Suma vectorial: $\mathbf{u}+\mathbf{v}=[u_1+v_1,u_2+v_2,\dots ,u_n+v_n]$

Multiplicación escalar: $c\mathbf{u}=[c{u}_1,c{u}_2,\dots ,c{u}_n]$

Resta vectorial: $\mathbf{u}-\mathbf{v}=\mathbf{u}+(-\mathbf{v})$

1.2 Propiedades Algebraicas en ${\mathbb{R}}^n$

Teorema - Propiedades Algebraicas de Vectores

Para todos $\mathbf{u},\mathbf{v},\mathbf{w}\in {\mathbb{R}}^n$ y escalares $c,d\in \mathbb{R}$:

1. Conmutatividad: $\mathbf{u}+\mathbf{v}=\mathbf{v}+\mathbf{u}$
2. Asociatividad: $(\mathbf{u}+\mathbf{v})+\mathbf{w}=\mathbf{u}+(\mathbf{v}+\mathbf{w})$
3. Elemento neutro: $\mathbf{u}+0=\mathbf{u}$
4. Elemento inverso: $\mathbf{u}+(-\mathbf{u})=0$
5. Distributividad escalar: $c(\mathbf{u}+\mathbf{v})=c\mathbf{u}+c\mathbf{v}$
6. Distributividad vectorial: $(c+d)\mathbf{u}=c\mathbf{u}+d\mathbf{u}$
7. Asociatividad escalar: $c(d\mathbf{u})=(cd)\mathbf{u}$
8. Identidad escalar: $1\mathbf{u}=\mathbf{u}$

---

2. El Producto Punto (Producto Escalar)

2.1 Definición Fundamental

Definición - Producto Punto

Si $\mathbf{u}=[u_1,u_2,\dots ,u_n]$ y $\mathbf{v}=[v_1,v_2,\dots ,v_n]$, entonces el producto punto de $\mathbf{u}$ y $\mathbf{v}$ se define como:

$\mathbf{u}\cdot \mathbf{v}=u_1{v}_1+u_2{v}_2+\cdots +u_n{v}_n$

Interpretación

El producto punto es la suma de los productos de las componentes correspondientes. El resultado es un número real (escalar), no un vector.

2.2 Ejemplos Básicos

Ejemplo 1 - Producto Punto en \mathbb{R}^2

Problema: Calcule $\mathbf{u}\cdot \mathbf{v}$ cuando $\mathbf{u}=[1,2]$ y $\mathbf{v}=[-3,5]$

Solución: $\mathbf{u}\cdot \mathbf{v}=1\cdot (-3)+2\cdot 5=-3+10=7$

Ejemplo 2 - Producto Punto en \mathbb{R}^3

Problema: Si $\mathbf{u}=[1,0,2]$ y $\mathbf{v}=[2,4,1]$, encuentre $\mathbf{u}\cdot \mathbf{v}$

Solución: $\mathbf{u}\cdot \mathbf{v}=1(2)+0(4)+2(1)=2+0+2=4$

2.3 Propiedades del Producto Punto

Teorema - Propiedades del Producto Punto

Sean $\mathbf{u},\mathbf{v},\mathbf{w}$ vectores en ${\mathbb{R}}^n$ y $c$ un escalar. Entonces:

a. $\mathbf{u}\cdot \mathbf{v}=\mathbf{v}\cdot \mathbf{u}$ (Conmutatividad)

b. $\mathbf{u}\cdot (\mathbf{v}+\mathbf{w})=\mathbf{u}\cdot \mathbf{v}+\mathbf{u}\cdot \mathbf{w}$ (Distributividad)

c. $(c\mathbf{u})\cdot \mathbf{v}=c(\mathbf{u}\cdot \mathbf{v})$

d. $\mathbf{u}\cdot \mathbf{u}\ge 0$ y $\mathbf{u}\cdot \mathbf{u}=0$ si y solo si $\mathbf{u}=0$

---

3. Longitud y Norma de Vectores

3.1 Definición de Longitud

Definición - Longitud (Norma) de un Vector

La longitud (o norma) de un vector $\mathbf{v}=[v_1,v_2,\dots ,v_n]$ en ${\mathbb{R}}^n$ es el escalar no negativo definido por:

$|\mathbf{v}|=\sqrt{\mathbf{v}\cdot \mathbf{v}}=\sqrt{v_1^2+v_2^2+\cdots +v_n^2}$

3.2 Conexión con el Teorema de Pitágoras

En ${\mathbb{R}}^2$ y ${\mathbb{R}}^3$, esta definición coincide con la distancia euclidiana familiar:

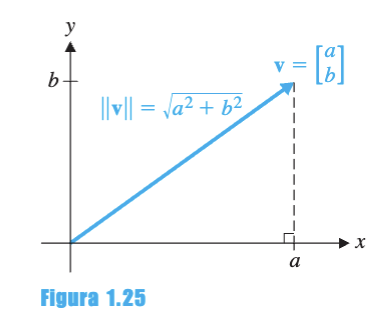
Interpretación Geométrica

Para $\mathbf{v}=[a,b]$ en ${\mathbb{R}}^2$, la longitud $|\mathbf{v}|=\sqrt{a^2+b^2}$ es la hipotenusa del triángulo rectángulo con catetos de longitud $|a|$ y $|b|$.

3.3 Ejemplos de Cálculo de Longitud

Ejemplo 3 - Longitud en \mathbb{R}^3

Problema: Encuentre la longitud del vector $\mathbf{v}=[2,-1,3]$

Solución: $|\mathbf{v}|=\sqrt{2^2+(-1{)}^2+3^2}=\sqrt{4+1+9}=\sqrt{14}$

3.4 Propiedades de la Longitud

Teorema - Propiedades de la Longitud

Sea $\mathbf{v}$ un vector en ${\mathbb{R}}^n$ y $c$ un escalar. Entonces:

a. $|\mathbf{v}|\ge 0$ y $|\mathbf{v}|=0$ si y solo si $\mathbf{v}=0$

b. $|c\mathbf{v}|=|c||\mathbf{v}|$

---

4. Vectores Unitarios

4.1 Definición

Definición - Vector Unitario

Un vector $\mathbf{u}$ es unitario si tiene longitud 1, es decir: $|\mathbf{u}|=1$

4.2 Vectores Unitarios Estándar

En ${\mathbb{R}}^n$, los vectores unitarios canónicos son:

${\mathbf{e}}_1=[1,0,0,\dots ,0],{\mathbf{e}}_2=[0,1,0,\dots ,0],\dots ,{\mathbf{e}}_n=[0,0,0,\dots ,1]$

Notación Especial

En ${\mathbb{R}}^2$: $\hat{\mathbf{i}}=[1,0]$ y $\hat{\mathbf{j}}=[0,1]$

En ${\mathbb{R}}^3$: $\hat{\mathbf{i}}=[1,0,0]$, $\hat{\mathbf{j}}=[0,1,0]$ y $\hat{\mathbf{k}}=[0,0,1]$

4.3 Normalización de Vectores

Definición - Normalización

Dado un vector no nulo $\mathbf{v}$, el vector unitario en la misma dirección que $\mathbf{v}$ está dado por:

$\mathbf{u}=\frac{\mathbf{v}}{|\mathbf{v}|}=\frac{1}{|\mathbf{v}|}\mathbf{v}$

Ejemplo 4 - Normalización

Problema: Normalice el vector $\mathbf{v}=[2,-1,3]$

Solución:

1. $|\mathbf{v}|=\sqrt{14}$ (calculado anteriormente)
2. $\mathbf{u}=\frac{1}{\sqrt{14}}[2,-1,3]=\left[\frac{2}{\sqrt{14}},\frac{-1}{\sqrt{14}},\frac{3}{\sqrt{14}}\right]$

---

5. Distancia entre Vectores

5.1 Definición

Definición - Distancia entre Vectores

La distancia $d(\mathbf{u},\mathbf{v})$ entre los vectores $\mathbf{u}$ y $\mathbf{v}$ en ${\mathbb{R}}^n$ se define por:

$d(\mathbf{u},\mathbf{v})=|\mathbf{u}-\mathbf{v}|$

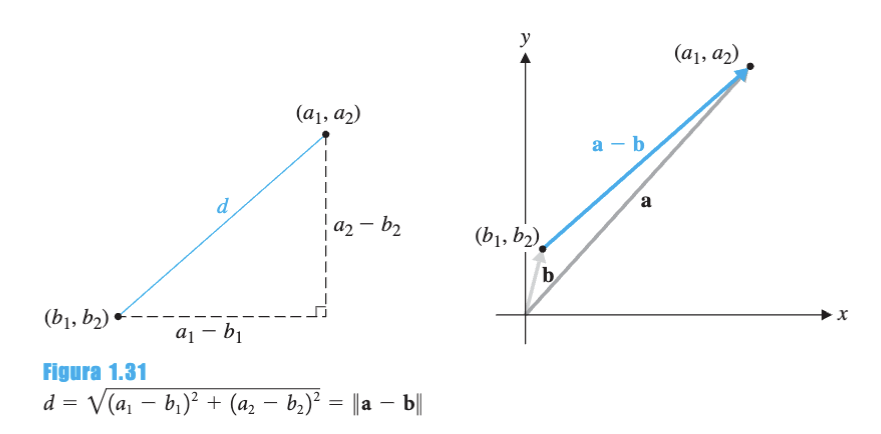
5.2 Ejemplo de Cálculo de Distancia

Ejemplo 5 - Distancia entre Vectores

Problema: Encuentre la distancia entre $\mathbf{u}=[2,1,-1]$ y $\mathbf{v}=[0,2,-2]$

Solución:

1. $\mathbf{u}-\mathbf{v}=[2-0,1-2,-1-(-2)]=[2,-1,1]$
2. $d(\mathbf{u},\mathbf{v})=|\mathbf{u}-\mathbf{v}|=\sqrt{2^2+(-1{)}^2+1^2}=\sqrt{6}$

---

6. Ángulos entre Vectores

6.1 Fórmula del Coseno

Para vectores no nulos $\mathbf{u}$ y $\mathbf{v}$ en ${\mathbb{R}}^n$, el ángulo $\theta$ entre ellos se relaciona con el producto punto mediante:

Teorema - Fórmula del Coseno para Vectores

$\cos \theta =\frac{\mathbf{u}\cdot \mathbf{v}}{|\mathbf{u}||\mathbf{v}|}$

donde $0\le \theta \le 180°$

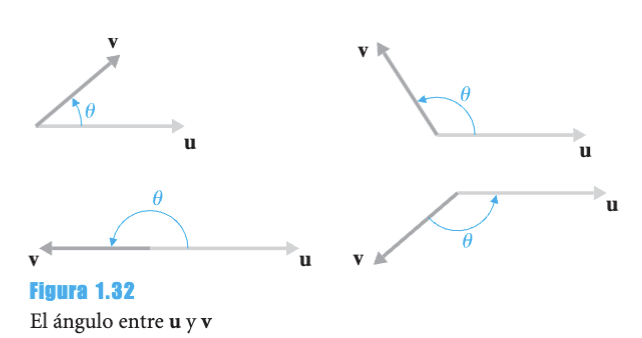
6.2 Definición Formal del Ángulo

Definición - Ángulo entre Vectores

Para vectores $\mathbf{u}$ y $\mathbf{v}$ distintos de cero en ${\mathbb{R}}^n$:

$\cos \theta =\frac{\mathbf{u}\cdot \mathbf{v}}{|\mathbf{u}||\mathbf{v}|}$

6.3 Ejemplo de Cálculo de Ángulo

Ejemplo 6 - Ángulo entre Vectores

Problema: Calcule el ángulo entre $\mathbf{u}=[2,1,-2]$ y $\mathbf{v}=[1,1,1]$

Solución:

1. $\mathbf{u}\cdot \mathbf{v}=2(1)+1(1)+(-2)(1)=1$
2. $|\mathbf{u}|=\sqrt{4+1+4}=3$
3. $|\mathbf{v}|=\sqrt{1+1+1}=\sqrt{3}$
4. $\cos \theta =\frac{1}{3\sqrt{3}}=\frac{\sqrt{3}}{9}$
5. $\theta ={\cos }^{-1}\left(\frac{\sqrt{3}}{9}\right)$

---

7. Vectores Ortogonales

7.1 Definición

Definición - Vectores Ortogonales

Los vectores $\mathbf{u}$ y $\mathbf{v}$ en ${\mathbb{R}}^n$ son ortogonales si su producto punto es cero:

$\mathbf{u}\cdot \mathbf{v}=0$

Interpretación Geométrica

Vectores ortogonales forman un ángulo de 90° entre ellos.

7.2 Propiedades de Vectores Ortogonales

Teorema de Pitágoras para Vectores

Si $\mathbf{u}$ y $\mathbf{v}$ son ortogonales, entonces:

$|\mathbf{u}+\mathbf{v}{|}^2=|\mathbf{u}{|}^2+|\mathbf{v}{|}^2$

7.3 Ejemplos de Ortogonalidad

Ejemplo 7 - Verificar Ortogonalidad

Problema: Determine si $\mathbf{u}=[1,-1,0]$ y $\mathbf{v}=[1,1,2]$ son ortogonales

Solución: $\mathbf{u}\cdot \mathbf{v}=1(1)+(-1)(1)+0(2)=1-1+0=0$

Por tanto, $\mathbf{u}$ y $\mathbf{v}$ son ortogonales.

---

8. Desigualdades Importantes

8.1 Desigualdad de Cauchy-Schwarz

Teorema - Desigualdad de Cauchy-Schwarz

Para todos los vectores $\mathbf{u}$ y $\mathbf{v}$ en ${\mathbb{R}}^n$:

$|\mathbf{u}\cdot \mathbf{v}|\le |\mathbf{u}||\mathbf{v}|$

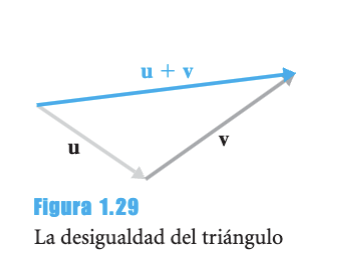
8.2 Desigualdad del Triángulo

Teorema - Desigualdad del Triángulo

Para todos los vectores $\mathbf{u}$ y $\mathbf{v}$ en ${\mathbb{R}}^n$:

$|\mathbf{u}+\mathbf{v}|\le |\mathbf{u}|+|\mathbf{v}|$

---

🚨 Errores Comunes

Error 1: Confundir producto punto con multiplicación escalar

• Incorrecto: Pensar que $\mathbf{u}\cdot \mathbf{v}$ es un vector
• Correcto: El producto punto siempre produce un escalar

Error 2: Aplicar producto punto a vectores de diferente dimensión

• Incorrecto: Intentar $[1,2]\cdot [3,4,5]$
• Correcto: Solo vectores de la misma dimensión pueden multiplicarse punto a punto

Error 3: Olvidar la raíz cuadrada en la longitud

• Incorrecto: $|\mathbf{v}|=\mathbf{v}\cdot \mathbf{v}$
• Correcto: $|\mathbf{v}|=\sqrt{\mathbf{v}\cdot \mathbf{v}}$

Error 4: Confundir ortogonalidad con paralelismo

• Incorrecto: Vectores ortogonales apuntan en la misma dirección
• Correcto: Vectores ortogonales son perpendiculares (ángulo de 90°)

---

Ejercicios Propuestos

Ejercicios de Práctica

1. Calcule $\mathbf{u}\cdot \mathbf{v}$ para $\mathbf{u}=[3,-2,1]$ y $\mathbf{v}=[1,4,-2]$
2. Encuentre la longitud del vector $\mathbf{w}=[1,-3,2,4]$
3. Normalice el vector $\mathbf{a}=[6,-8,0]$
4. Determine si los vectores $[2,1,-1]$ y $[1,-2,0]$ son ortogonales
5. Calcule el ángulo entre $[1,0,1]$ y $[0,1,1]$
6. Verifique la desigualdad de Cauchy-Schwarz para vectores específicos

---

🎯 Conceptos Clave para Repasar

Resumen de Conceptos

1. Producto punto: Operación que produce un escalar a partir de dos vectores
2. Longitud/Norma: Magnitud de un vector, calculada usando el producto punto
3. Vector unitario: Vector de longitud 1, obtenido por normalización
4. Distancia: Longitud del vector diferencia entre dos puntos
5. Ángulo: Determinado por la fórmula del coseno usando producto punto
6. Ortogonalidad: Vectores perpendiculares tienen producto punto cero
7. Desigualdades: Cauchy-Schwarz y triangular son fundamentales

---

✅ Checklist de Estudio

Lista de Verificación

• Puedo calcular productos punto en cualquier dimensión
• Sé encontrar la longitud de cualquier vector
• Comprendo cómo normalizar vectores
• Puedo calcular distancias entre puntos
• Sé determinar ángulos entre vectores
• Reconozco cuándo dos vectores son ortogonales
• Entiendo las desigualdades de Cauchy-Schwarz y del triángulo
• Puedo aplicar estas herramientas en problemas geométricos

---

📚 Referencias

Lectura Principal

• Poole, D. Álgebra lineal: Una introducción moderna. Sección 1.2, págs. 18-24
• Lay, D. Álgebra Lineal y sus Aplicaciones. Sección 6.1, págs. 331-338

Temas Relacionados

• Vector - Concepto fundamental
• Combinacion-Lineal - Operaciones con vectores
• Vectores-Unitarios - Vectores de longitud uno

---

🏷️ Tags

algebra-lineal producto-punto vectores longitud-vectores angulos ortogonalidad vectores-unitarios distancia cauchy-schwarz desigualdad-triangular normalizacion clase-02 clase

---

Próxima Clase

En la Clase 03, estudiaremos ecuaciones lineales y sistemas matriciales, aplicando los conceptos de vectores para resolver problemas más complejos.