Clase 19: Razones de Cambio y Razones Relacionadas
📚 Introducción
Esta clase conecta el concepto abstracto de derivada con aplicaciones concretas en física, economía, y otras ciencias. La razón de cambio es simplemente otra forma de interpretar la derivada: nos indica qué tan rápido cambia una cantidad respecto a otra. Las razones relacionadas nos permiten encontrar la velocidad de cambio de una variable cuando conocemos la velocidad de cambio de otra variable relacionada.
Objetivos de la Clase
- Interpretar la derivada como razón de cambio en diferentes contextos
- Aplicar razones de cambio en física: velocidad y aceleración
- Aplicar razones de cambio en economía: costo marginal, ingreso marginal
- Resolver problemas de razones relacionadas mediante la regla de la cadena
- Identificar y relacionar variables que cambian simultáneamente
1. Concepto de Razón de Cambio
1.1 Definición de Razon-de-Cambio
Definición - Razón de Cambio
Si , entonces la derivada representa la razón de cambio instantánea de respecto a .
Esto significa que indica qué tan rápido cambia cuando cambia.
1.2 Razón de Cambio Promedio vs Instantánea
La razón de cambio promedio de entre y es:
La razón de cambio instantánea en es:
Observación
La razón de cambio promedio es la pendiente de la recta secante, mientras que la razón de cambio instantánea es la pendiente de la recta tangente.
2. Aplicaciones en Física
2.1 Velocidad y Aceleración
Definiciones en Física
Si es la función posición de un objeto que se mueve en línea recta:
- Velocidad instantánea:
- Aceleración instantánea:
Interpretación física:
- La velocidad es la razón de cambio de la posición respecto al tiempo
- La aceleración es la razón de cambio de la velocidad respecto al tiempo
- La aceleración también es la segunda derivada de la posición
2.2 Ejemplo: Movimiento Rectilíneo
Ejemplo - Partícula en Movimiento
La posición de una partícula está dada por , donde se mide en segundos y en metros.
a) Encuentre la velocidad en el instante
b) ¿Cuál es la velocidad después de 2 y 4 segundos?
- m/s
- m/s
c) ¿Cuándo está en reposo la partícula?
En reposo cuando :
La partícula está en reposo en s y s
d) Halle la aceleración
3. Aplicaciones en Economía
3.1 Costo Marginal
Definición - Costo-Marginal
Si es el costo total de producir unidades de un artículo, entonces el costo marginal es:
Representa el costo aproximado de producir una unidad adicional.
3.2 Otras Funciones Marginales
- Ingreso marginal: (razón de cambio del ingreso)
- Utilidad marginal: (razón de cambio de la utilidad)
Donde es la función utilidad.
3.3 Ejemplo: Costo Marginal
Ejemplo - Función de Costo
Una compañía ha estimado que el costo (en dólares) de producir artículos es:
a) Encuentre la función de costo marginal
b) El costo marginal en el nivel de producción de 500 artículos es:
15$ /artículo
Esto significa que cuando , el costo se incrementa aproximadamente $15 por cada artículo adicional producido.
c) Compare con el costo real del artículo 501:
Costo real:
El costo marginal es una buena aproximación del costo real.
4. Razones Relacionadas
4.1 Concepto de Razones-Relacionadas
Idea Principal
En problemas de razones relacionadas:
- Dos o más cantidades cambian con el tiempo
- Estas cantidades están relacionadas por una ecuación
- Conocemos la razón de cambio de una cantidad
- Queremos encontrar la razón de cambio de otra cantidad
4.2 Estrategia para Resolver Problemas
Método para Razones Relacionadas
Paso 1: Lea cuidadosamente el problema e identifique:
- ¿Qué cantidades cambian con el tiempo?
- ¿Qué razón de cambio se conoce?
- ¿Qué razón de cambio se busca?
Paso 2: Dibuje un diagrama si es posible
Paso 3: Introduzca notación. Asigne símbolos a todas las cantidades que varían con el tiempo
Paso 4: Exprese la información dada y la razón requerida en términos de derivadas
Paso 5: Escriba una ecuación que relacione las variables
Paso 6: Derive implícitamente respecto a usando la regla de la cadena
Paso 7: Sustituya la información numérica dada y resuelva para la razón desconocida
4.3 Ejemplo: Escalera Resbalando
Ejemplo - Escalera contra Pared
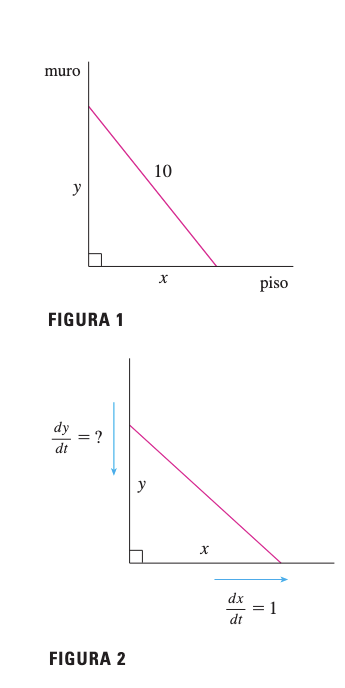
Una escalera de 10 pies de largo está apoyada contra un muro vertical. Si la parte inferior se desliza alejándose de la pared a razón de 1 pie/s, ¿qué tan rápido resbala hacia abajo por la pared la parte superior cuando la parte inferior está a 6 pies del muro?
Paso 1-3: Dibujamos y definimos:
- = distancia desde la base de la escalera al muro
- = distancia desde el suelo a la parte superior de la escalera
- Conocido: pie/s cuando
- Buscar: cuando
Paso 5: Por el teorema de Pitágoras:
Paso 6: Derivar respecto a :
Paso 7: Cuando :
La parte superior baja a razón de 3/4 pies/s (negativo indica descenso).
4.4 Ejemplo: Globo Inflándose
Ejemplo del Libro (pág. 224)
Se infla un globo esférico y su volumen crece a razón de 100 cm³/s. ¿Qué tan rápido aumenta el radio del globo cuando el diámetro es de 50 cm?
Datos:
- Conocido: cm³/s
- Buscar: cuando cm
Relación:
Derivar:
Resolver:
Cuando :
5. Otras Aplicaciones en Ciencias
5.1 Biología
Crecimiento de Población
Si es el número de individuos de una población en el tiempo , entonces:
Para población de bacterias que se duplica cada hora:
5.2 Química
Velocidad de Reacción
Para una reacción , si denota la concentración del producto:
5.3 Física - Flujo de Sangre
Ley de Poiseuille
El flujo de sangre por un vaso sanguíneo es proporcional a , donde es el radio:
La razón de cambio del flujo respecto al radio:
🎯 Conceptos Clave para Repasar
Resumen de Conceptos
- Razón de cambio instantánea: Es la derivada
- Velocidad: Primera derivada de la posición
- Aceleración: Segunda derivada de la posición
- Costo marginal: Derivada del costo
- Razones relacionadas: Usar regla de la cadena para relacionar y
- Estrategia: Identificar variables, relacionarlas, derivar implícitamente respecto a
🚨 Errores Comunes
Error 1: Confundir razón promedio con instantánea
- Incorrecto: Usar cuando se pide la razón instantánea
- Correcto: Calcular la derivada para razón instantánea
Error 2: No derivar respecto a la variable correcta
- Incorrecto: En razones relacionadas, derivar solo respecto a
- Correcto: Derivar respecto a usando regla de la cadena
Error 3: Sustituir valores antes de derivar
- Incorrecto: Reemplazar antes de derivar la ecuación
- Correcto: Primero derivar, luego sustituir los valores numéricos
Error 4: Olvidar el signo
- Incorrecto: Ignorar si la cantidad aumenta (+) o disminuye (-)
- Correcto: Interpretar el signo de según el contexto
📝 Ejercicios Propuestos
Ejercicios de Práctica
Física:
- Ejemplo 1, pág. 224: Posición de partícula y cálculo de velocidad/aceleración
- Ejemplo 8, pág. 231: Movimiento de proyectil
Economía: 3. Ejemplo 2, pág. 245: Costo marginal de producción 4. Ejemplo 3, pág. 245: Ingreso marginal y utilidad marginal
Razones Relacionadas: 5. Escalera de 10 pies resbalando (ejemplo trabajado en clase) 6. Globo esférico inflándose (Ejemplo del libro) 7. Dos autos aproximándose a una intersección 8. Nivel de agua subiendo en un tanque cónico
📚 Referencias
Lectura Principal
- Sección 3.7: Razones de cambio en las ciencias sociales y naturales, págs. 224-233
- Sección 3.9: Razones relacionadas, pág 244-248
Enlaces Relacionados
- 11) Razón de Cambio Promedio y Razón de Cambio Instantánea - Introducción al concepto
- Regla-de-la-Cadena - Técnica clave para razones relacionadas
- Derivacion-Implicita - Necesaria para derivar ecuaciones
Sugerencia de Estudio
Las razones relacionadas requieren práctica para dominar la estrategia. No intentes memorizar procedimientos específicos para cada tipo de problema. En su lugar, enfócate en entender:
- Cómo identificar las variables que cambian
- Cómo relacionarlas mediante una ecuación
- Cómo aplicar la regla de la cadena al derivar respecto al tiempo
Clave del éxito: Siempre pregúntate “¿qué está cambiando y con qué rapidez?”
✅ Checklist de Estudio
Lista de Verificación
- Puedo interpretar la derivada como razón de cambio en diferentes contextos
- Comprendo la diferencia entre velocidad y aceleración
- Puedo calcular funciones marginales (costo, ingreso, utilidad)
- Entiendo cuándo usar razones relacionadas
- Sé identificar todas las variables que cambian con el tiempo
- Puedo derivar implícitamente respecto al tiempo
- Comprendo cuándo sustituir valores numéricos (después de derivar)
- Puedo interpretar el significado del signo en
🏷️ Tags
calculo razones-de-cambio razones-relacionadas derivadas-aplicadas fisica economia velocidad aceleracion costo-marginal clase-19