Clase 01: Geometría y Algebra de Vectores
📚 Introducción
Esta clase introduce los conceptos fundamentales de vectores en el plano y el espacio, estableciendo las bases geométricas y algebraicas necesarias para el estudio del álgebra lineal.
1. Concepto de Vector
1.1 Definición Fundamental
Un Vector es un segmento de recta dirigido que posee tres características esenciales:
- Magnitud (longitud)
- Dirección
- Sentido
1.2 Notación
- El vector de A a B se denota:
- A: Punto inicial u origen
- B: Punto terminal o punta
- También se puede denotar por una letra minúscula en negrita: v

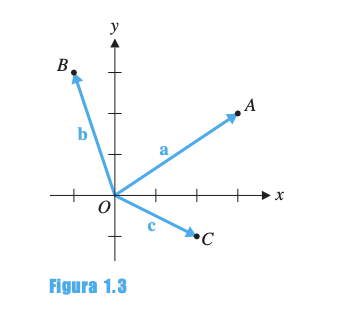
1.3 Vectores de Posición
Los vectores de posición son aquellos con origen en el punto (origen del sistema coordenado):
- A cada punto le corresponde el vector
- A cada vector a con origen en le corresponde su punta
2. Vectores en el Plano ()
2.1 Representación por Coordenadas
Los vectores en el plano se representan usando coordenadas:
- Si , entonces
- Se usan corchetes para distinguir vectores de puntos
2.2 Componentes de un Vector
- Las coordenadas individuales se llaman componentes del vector
- Para :
- Primera componente: 3
- Segunda componente: 2
2.3 Igualdad de Vectores
Definición: Dos vectores son iguales si y solo si:
- Sus componentes correspondientes son iguales
- Tienen la misma longitud y dirección
- Coinciden al desplazar uno paralelamente al otro
Ejemplo: implica que y
2.4 Desplazamiento y Traslación
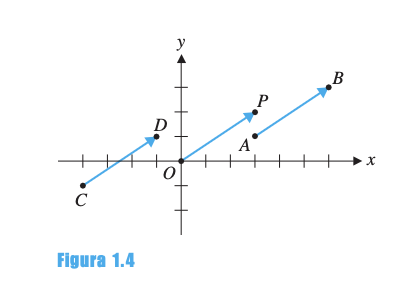
Dos vectores y son iguales si representan el mismo desplazamiento:
Por tanto,
Nota: Un vector en posición estándar es aquel con punto inicial en el origen. Todo vector puede representarse en posición estándar mediante traslación.
3. Tipos de Vectores
3.1 Vectores Columna
Representación como matriz de una columna:
- Mejor representación computacional
- y son las componentes del vector
3.2 Vectores Renglón
Representación como matriz de una fila:
3.3 Vector Cero (Nulo)
Vector con magnitud cero, sin dirección ni sentido:
4. Operaciones con Vectores
4.1 Suma de Vectores
Si y , entonces:
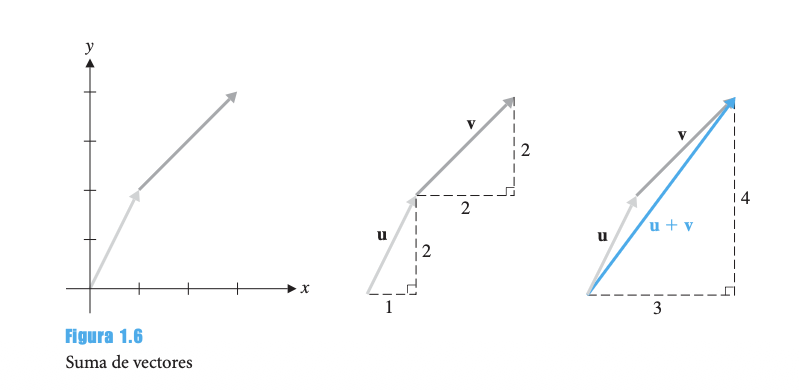
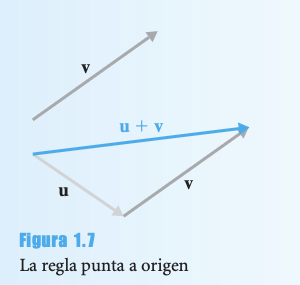
Regla Punta a Origen
- Traslade v de modo que su origen coincida con la punta de u
- La suma es el vector desde el origen de u hasta la punta de v
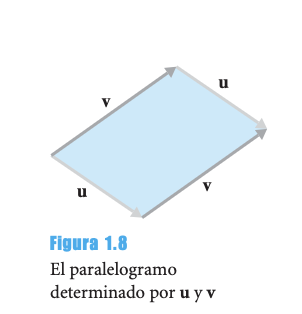
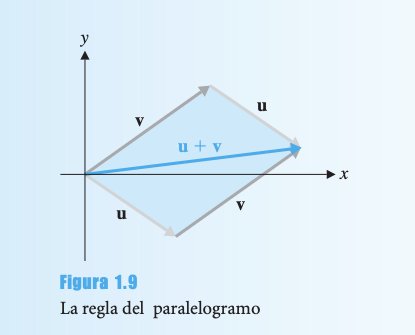
Regla del Paralelogramo
Para vectores en posición estándar, es la diagonal del paralelogramo determinado por u y v.
4.2 Multiplicación Escalar
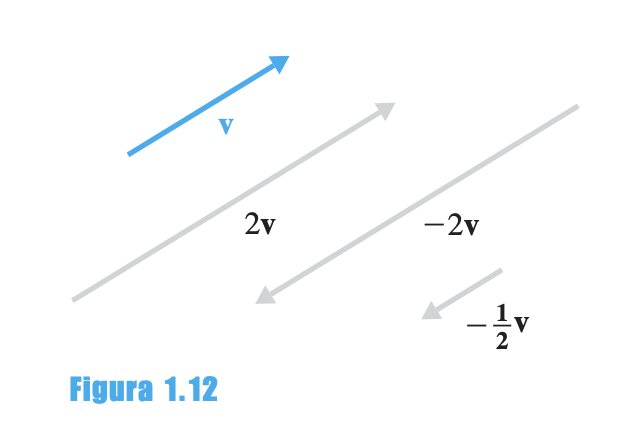
Dado un vector y un escalar :
Propiedades geométricas:
- Si : mismo sentido que v
- Si : sentido opuesto a v
- (magnitud)
4.3 Resta de Vectores
El negativo de v es:
La diferencia entre u y v es:
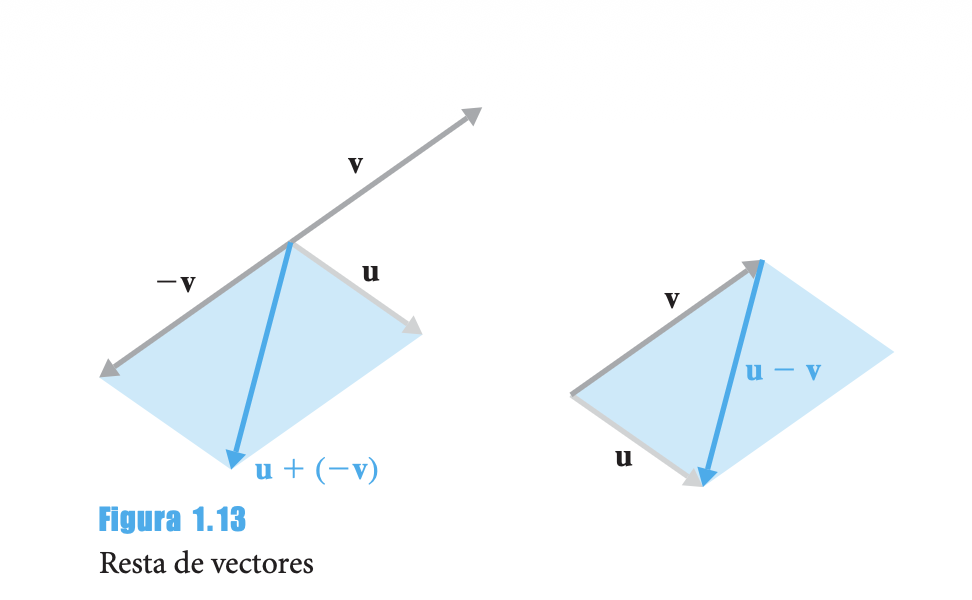
Observación: corresponde a la otra diagonal del paralelogramo determinado por u y v.
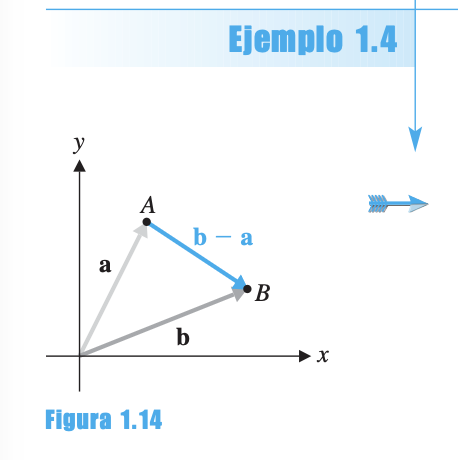
Si los puntos y corresponden a vectores a y b en posición estándar:
5. Vectores Unitarios
5.1 Definición
Vectores-Unitarios: Vectores con magnitud igual a 1 que indican únicamente dirección.
5.2 Vectores Unitarios Estándar
En :
- - dirección positiva del eje X
- - dirección positiva del eje Y
En :
- - dirección positiva del eje Z
5.3 Descomposición en Vectores Unitarios
Todo vector en se puede expresar como:
En general:
donde son los vectores unitarios canónicos.
6. Vectores en Tres Dimensiones ()
6.1 Sistema de Coordenadas
El espacio tridimensional utiliza tres ejes coordenados mutuamente perpendiculares:
- Eje X
- Eje Y
- Eje Z
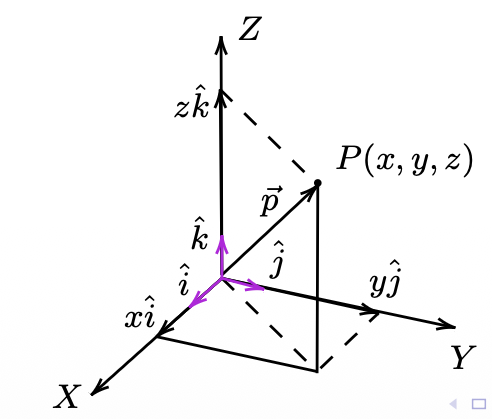
6.2 Localización de Puntos y Vectores
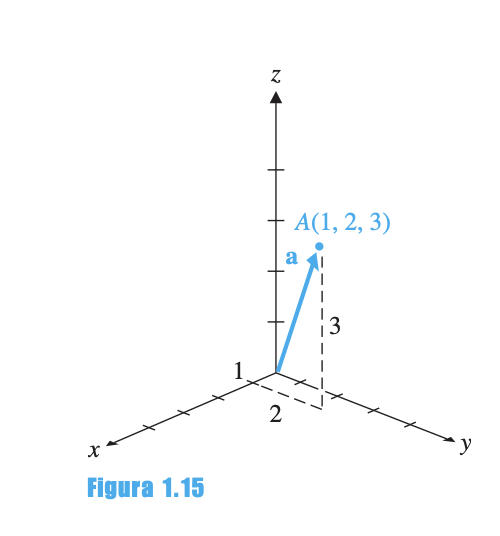
Para localizar :
- Recorrer 1 unidad en el eje X
- Avanzar 2 unidades paralelas al eje Y
- Mover 3 unidades paralelas al eje Z
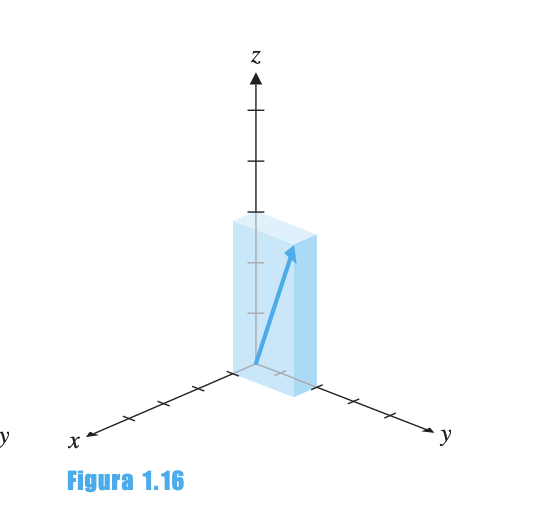
6.3 Visualización mediante Caja
El vector corresponde a la diagonal desde el origen hasta la esquina opuesta de una caja determinada por los planos coordenados.
7. Vectores en
7.1 Definición General
es el conjunto de todas las n-adas ordenadas de números reales:
- : componente i-ésimo del vector
7.2 Operaciones en
Para y :
- Suma: componente i-ésimo es
- Multiplicación escalar: componente i-ésimo es
⚠️ Importante: No suponer que la aritmética vectorial será idéntica a la de números reales. Verificar siempre las propiedades algebraicas antes de usarlas.
8. Propiedades Algebraicas de Vectores
8.1 Conmutatividad de la Suma
La propiedad se verifica geométricamente:
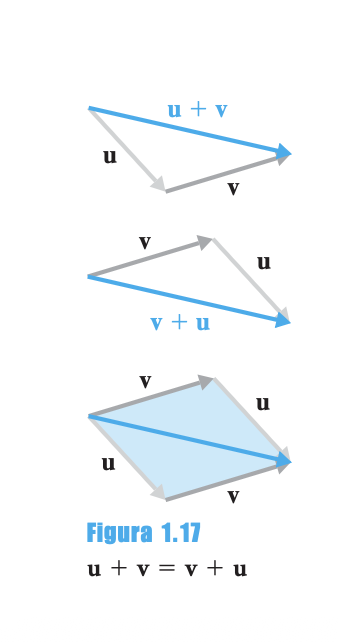
Ambas sumas producen la misma diagonal del paralelogramo.
8.2 Propiedades Fundamentales en
Para todos y escalares :
| Propiedad | Expresión | Nombre |
|---|---|---|
| 1 | Conmutatividad | |
| 2 | Asociatividad | |
| 3 | Elemento neutro | |
| 4 | Elemento inverso | |
| 5 | Distributividad escalar | |
| 6 | Distributividad vectorial | |
| 7 | Asociatividad escalar | |
| 8 | Identidad escalar |

9. Combinaciones Lineales
9.1 Definición
Dados vectores en y escalares :
se llama Combinacion-Lineal de los vectores con pesos .
9.2 Ejemplos de Combinaciones Lineales
Para vectores y :
Nota: Los pesos pueden ser cualquier número real, incluyendo cero.
🎯 Conceptos Clave para Repasar
- Vector: Entidad con magnitud, dirección y sentido
- Componentes: Coordenadas que definen un vector
- Posición estándar: Vector con origen en O
- Operaciones básicas: Suma, resta, multiplicación escalar
- Vectores unitarios: Base para descomposición
- Combinación lineal: Construcción fundamental en álgebra lineal
📚 Referencias
- Poole, D. Álgebra lineal: Una introducción moderna. Sección 1.1, págs. 3-9
- Lay, D. Álgebra Lineal y sus Aplicaciones. Sección 1.3, pág. 24
🏷️ Tags
algebra-lineal vectores vectores-geometricos R2 R3 Rn operaciones-vectoriales combinaciones-lineales vectores-unitarios clase