12) Independencia Lineal

Clase 12: Independencia Lineal

---

📋 Resumen Ejecutivo

Objetivos de la Clase

En esta clase aprenderás a:

• Comprender el concepto de independencia lineal
• Determinar si un conjunto de vectores es linealmente independiente
• Relacionar independencia lineal con sistemas homogéneos
• Identificar relaciones de dependencia entre vectores
• Aplicar criterios para verificar independencia lineal

Idea Central

Un conjunto de vectores es linealmente independiente si ninguno de ellos puede expresarse como combinación lineal de los demás. Esta propiedad es fundamental para entender bases, dimensión y la estructura de espacios vectoriales.

---

1. Motivación y Definición

1.1 Pregunta Motivadora

¿Cuándo un Vector es "Redundante"?

Consideremos los vectores en ${\mathbb{R}}^3$:

${\mathbf{v}}_1=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right],{\mathbf{v}}_2=\left[\begin{array}{c}4\\ 5\\ 6\end{array}\right],{\mathbf{v}}_3=\left[\begin{array}{c}2\\ 1\\ 0\end{array}\right]$

¿Existe alguna relación especial entre ellos? ¿Alguno se puede expresar en términos de los otros?

1.2 Definición Formal

Definición - Independencia Lineal

Se dice que un conjunto indexado de vectores $\{{\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_p\}$ en ${\mathbb{R}}^n$ es linealmente independiente si la ecuación vectorial:

$x_1{\mathbf{v}}_1+x_2{\mathbf{v}}_2+\cdots +x_p{\mathbf{v}}_p=0$

solo tiene la solución trivial $x_1=x_2=\cdots =x_p=0$.

Definición - Dependencia Lineal

Se dice que el conjunto $\{{\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_p\}$ es linealmente dependiente si existen pesos $c_1,c_2,\dots ,c_p$, no todos cero, tales que:

$c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2+\cdots +c_p{\mathbf{v}}_p=0$

Esta ecuación se llama relación de dependencia lineal entre ${\mathbf{v}}_1,\dots ,{\mathbf{v}}_p$.

1.3 Interpretación

¿Qué Significa Realmente?

Linealmente independiente: Ningún vector del conjunto puede escribirse como combinación lineal de los demás.

Linealmente dependiente: Al menos un vector puede expresarse como combinación lineal de los otros (existe “redundancia”).

---

2. Ejemplos Fundamentales

2.1 Ejemplo Básico en ${\mathbb{R}}^3$

Ejemplo 1 - Determinando Independencia

Sean ${\mathbf{v}}_1=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]$, ${\mathbf{v}}_2=\left[\begin{array}{c}4\\ 5\\ 6\end{array}\right]$, ${\mathbf{v}}_3=\left[\begin{array}{c}2\\ 1\\ 0\end{array}\right]$

¿Es $\{{\mathbf{v}}_1,{\mathbf{v}}_2,{\mathbf{v}}_3\}$ linealmente independiente?

Solución:

Debemos determinar si existe una solución no trivial de: $x_1\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]+x_2\left[\begin{array}{c}4\\ 5\\ 6\end{array}\right]+x_3\left[\begin{array}{c}2\\ 1\\ 0\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$

Esto equivale al sistema:

$$\{\begin{array}{l}{x}_1+4x_2+2x_3=0\\ 2x_1+5x_2+x_3=0\\ 3x_1+6x_2+0x_3=0\end{array}$$

Formamos la matriz de coeficientes y reducimos:

$$\left[\begin{array}{ccc}1& 4& 2\\ 2& 5& 1\\ 3& 6& 0\end{array}\right]\sim \left[\begin{array}{ccc}1& 4& 2\\ 0& -3& -3\\ 0& 0& 0\end{array}\right]\sim \left[\begin{array}{ccc}1& 0& -2\\ 0& 1& 1\\ 0& 0& 0\end{array}\right]$$

Como $x_3$ es variable libre, hay soluciones no triviales. Por ejemplo, con $x_3=1$: $x_1=2,x_2=-1,x_3=1$

Verificación: $2{\mathbf{v}}_1-{\mathbf{v}}_2+{\mathbf{v}}_3=0$

Conclusión: Los vectores son linealmente dependientes.

Interpretación: Podemos despejar: ${\mathbf{v}}_3=-2{\mathbf{v}}_1+{\mathbf{v}}_2$, lo que muestra que ${\mathbf{v}}_3$ es “redundante”.

2.2 Ejemplo de Independencia Lineal

Ejemplo 2 - Vectores Independientes

Sean ${\mathbf{v}}_1=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$, ${\mathbf{v}}_2=\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$, ${\mathbf{v}}_3=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$

Consideremos: $x_1{\mathbf{v}}_1+x_2{\mathbf{v}}_2+x_3{\mathbf{v}}_3=0$

$x_1\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]+x_2\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]+x_3\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$

Claramente, la única solución es $x_1=x_2=x_3=0$.

Conclusión: Los vectores canónicos son linealmente independientes.

---

3. Método Matricial

3.1 Procedimiento Estándar

Criterio Matricial para Independencia Lineal

Para determinar si los vectores $\{{\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_p\}$ son linealmente independientes:

1. Forme la matriz $A=[{\mathbf{v}}_1{\mathbf{v}}_2\cdots {\mathbf{v}}_p]$ (vectores como columnas)
2. Resuelva el sistema homogéneo $A\mathbf{x}=0$
3. Linealmente independiente ⟺ Solo tiene la solución trivial ⟺ No hay variables libres
4. Linealmente dependiente ⟺ Tiene soluciones no triviales ⟺ Hay al menos una variable libre

3.2 Relación con Forma Escalonada

Criterio Práctico

Al reducir la matriz $A$ a forma escalonada:

• Independiente: Cada columna tiene posición pivote (todas las columnas son columnas pivote)
• Dependiente: Al menos una columna no tiene posición pivote (hay columna no pivote)

---

4. Teoremas Importantes

4.1 Caracterización de Dependencia

Teorema 7 - Caracterización de Dependencia Lineal

Un conjunto indexado $\{{\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_p\}$ de dos o más vectores es linealmente dependiente si y solo si al menos uno de los vectores es una combinación lineal de los demás.

De hecho, si $\{{\mathbf{v}}_1,\dots ,{\mathbf{v}}_p\}$ es linealmente dependiente y ${\mathbf{v}}_1\ne 0$, entonces algún ${\mathbf{v}}_j$ (con $j>1$) es combinación lineal de los vectores precedentes ${\mathbf{v}}_1,\dots ,{\mathbf{v}}_{j-1}$.

4.2 Casos Especiales

Teoremas de Casos Especiales

Teorema 8 - Dos Vectores: Un conjunto de dos vectores $\{{\mathbf{v}}_1,{\mathbf{v}}_2\}$ es linealmente dependiente si y solo si uno es múltiplo escalar del otro.

Teorema 9 - Vector Cero: Si un conjunto contiene el vector cero, entonces el conjunto es linealmente dependiente.

Razón: Si ${\mathbf{v}}_1=0$, entonces $1\cdot {\mathbf{v}}_1+0\cdot {\mathbf{v}}_2+\cdots =0$ es una relación de dependencia con peso no nulo.

4.3 Teorema del Tamaño

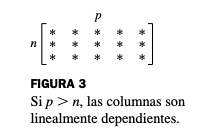
Teorema 10 - Demasiados Vectores

Si un conjunto contiene más vectores que entradas en cada vector, entonces el conjunto es linealmente dependiente.

En símbolos: Si $\{{\mathbf{v}}_1,\dots ,{\mathbf{v}}_p\}$ en ${\mathbb{R}}^n$ con $p>n$, entonces el conjunto es linealmente dependiente.

Razón: El sistema $A\mathbf{x}=0$ tiene $n$ ecuaciones y $p$ variables. Si $p>n$, hay al menos $p-n\ge 1$ variables libres, por lo que existen soluciones no triviales.

4.3 Dependencia lineal Visualmente

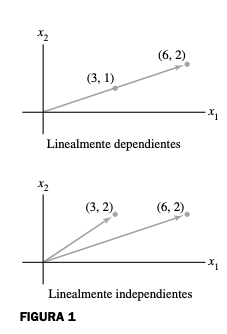
En ${\mathbb{R}}^2$

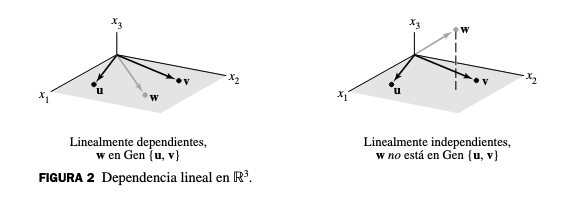
En ${\mathbb{R}}^3$

---

5. Ejemplos Desarrollados

5.1 Aplicando el Método Matricial

Ejemplo 3 - Análisis Completo

Determine si los vectores son linealmente independientes:

${\mathbf{v}}_1=\left[\begin{array}{c}1\\ -2\\ 3\end{array}\right],{\mathbf{v}}_2=\left[\begin{array}{c}5\\ -13\\ -3\end{array}\right],{\mathbf{v}}_3=\left[\begin{array}{c}0\\ -5\\ 2\end{array}\right]$

Solución:

Formamos la matriz y reducimos:

$A=\left[\begin{array}{ccc}1& 5& 0\\ -2& -13& -5\\ 3& -3& 2\end{array}\right]$

Reducción por filas:

$\left[\begin{array}{ccc}1& 5& 0\\ -2& -13& -5\\ 3& -3& 2\end{array}\right]\stackrel{R_2+2R_1}{\to }\left[\begin{array}{ccc}1& 5& 0\\ 0& -3& -5\\ 3& -3& 2\end{array}\right]\stackrel{R_3-3R_1}{\to }\left[\begin{array}{ccc}1& 5& 0\\ 0& -3& -5\\ 0& -18& 2\end{array}\right]$

$\stackrel{R_3-6R_2}{\to }\left[\begin{array}{ccc}1& 5& 0\\ 0& -3& -5\\ 0& 0& 32\end{array}\right]$

Tenemos 3 posiciones pivote (una en cada columna), por lo que no hay variables libres.

Conclusión: Los vectores son linealmente independientes.

5.2 Encontrando una Relación de Dependencia

Ejemplo 4 - Expresar un Vector como Combinación

Para los vectores del Ejemplo 1, encontramos que $2{\mathbf{v}}_1-{\mathbf{v}}_2+{\mathbf{v}}_3=0$.

Despejando: ${\mathbf{v}}_3=-2{\mathbf{v}}_1+{\mathbf{v}}_2$

Alternativamente: ${\mathbf{v}}_2=2{\mathbf{v}}_1+{\mathbf{v}}_3$

O: ${\mathbf{v}}_1=\frac{1}{2}{\mathbf{v}}_2-\frac{1}{2}{\mathbf{v}}_3$

Todas estas expresiones son equivalentes y muestran la dependencia lineal.

---

6. Interpretación Geométrica

6.1 En ${\mathbb{R}}^2$

Visualización en el Plano

Dos vectores en ${\mathbb{R}}^2$:

• Independientes: No son paralelos (apuntan en direcciones diferentes)
• Dependientes: Son paralelos (uno es múltiplo del otro)

Tres o más vectores en ${\mathbb{R}}^2$: Siempre son dependientes (por Teorema 10)

6.2 En ${\mathbb{R}}^3$

Visualización en el Espacio

Dos vectores en ${\mathbb{R}}^3$:

• Independientes: No son paralelos
• Dependientes: Son paralelos

Tres vectores en ${\mathbb{R}}^3$:

• Independientes: No son coplanares (no están en el mismo plano)
• Dependientes: Son coplanares

Cuatro o más vectores en ${\mathbb{R}}^3$: Siempre son dependientes (por Teorema 10)

---

7. Conexión con Columnas de una Matriz

Columnas e Independencia Lineal

Las columnas de una matriz $A$ son linealmente independientes si y solo si la ecuación $A\mathbf{x}=0$ tiene únicamente la solución trivial.

Equivalentemente:

• Las columnas de $A$ son linealmente independientes
• ⟺ Cada columna de $A$ es una columna pivote
• ⟺ La forma escalonada reducida de $A$ no tiene columnas sin pivote
• ⟺ El sistema $A\mathbf{x}=0$ no tiene variables libres

---

🚨 Errores Comunes

Error 1: Confundir independencia con ortogonalidad

• Incorrecto: “Vectores independientes son perpendiculares”
• Correcto: Independencia es algebraica, no geométrica. Vectores pueden ser independientes sin ser perpendiculares.

Error 2: Malinterpretar la solución trivial

• Incorrecto: “La solución trivial significa que el sistema no tiene solución”
• Correcto: La solución trivial es $x_1=x_2=\cdots =0$, y queremos que sea la ÚNICA solución.

Error 3: Olvidar verificar todos los coeficientes

• Incorrecto: En $c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2=0$, asumir dependencia si algún $c_i=0$
• Correcto: Para dependencia, al menos uno de los $c_i$ debe ser no nulo, pero no necesariamente todos.

Error 4: Aplicar mal el Teorema 10

• Incorrecto: “3 vectores en ${\mathbb{R}}^4$ son dependientes”
• Correcto: El teorema dice: más vectores QUE entradas (4 vectores en ${\mathbb{R}}^3$ son dependientes)

---

📝 Ejercicios de Práctica

Ejercicios Básicos

Problemas Fundamentales

1. Identificación directa: Sin hacer cálculos, determine si cada conjunto es linealmente dependiente:

   a) $\left\{\left[\begin{array}{c}1\\ 0\end{array}\right],\left[\begin{array}{c}0\\ 0\end{array}\right]\right\}$

   b) $\left\{\left[\begin{array}{c}3\\ -1\end{array}\right],\left[\begin{array}{c}-9\\ 3\end{array}\right]\right\}$

   c) Cuatro vectores en ${\mathbb{R}}^3$

2. Verificación de relación: Verifique que $\left[\begin{array}{c}2\\ 1\\ 0\end{array}\right]=3\left[\begin{array}{c}1\\ 0\\ 1\end{array}\right]-\left[\begin{array}{c}1\\ -1\\ 3\end{array}\right]$ y explique qué implica esto sobre la independencia lineal.

3. Método matricial simple: Determine si los vectores son linealmente independientes: $\left[\begin{array}{c}1\\ -1\\ 2\end{array}\right],\left[\begin{array}{c}0\\ 1\\ 1\end{array}\right]$

Ejercicios Intermedios

Práctica de Técnicas

4. Análisis completo: Para cada conjunto, determine si es linealmente independiente. Si es dependiente, encuentre una relación de dependencia.

   a) $\left\{\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right],\left[\begin{array}{c}-1\\ 0\\ 1\end{array}\right],\left[\begin{array}{c}3\\ 4\\ 5\end{array}\right]\right\}$

   b) $\left\{\left[\begin{array}{c}1\\ 0\\ 1\\ 0\end{array}\right],\left[\begin{array}{c}0\\ 1\\ 0\\ 1\end{array}\right],\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]\right\}$

5. Interpretación de forma escalonada: Una matriz $A$ de $4\times 5$ tiene forma escalonada: $\left[\begin{array}{ccccc}\bullet & \ast & \ast & 0& \ast \\ 0& 0& \bullet & 0& \ast \\ 0& 0& 0& \bullet & \ast \\ 0& 0& 0& 0& 0\end{array}\right]$ ¿Qué columnas de $A$ forman un conjunto linealmente independiente?

6. Construcción: Construya un conjunto de exactamente 3 vectores en ${\mathbb{R}}^4$ que sean linealmente dependientes, pero tales que cualquier subconjunto de 2 vectores sea linealmente independiente.

Ejercicios Avanzados

Problemas Conceptuales

7. Demostración: Si $\{{\mathbf{v}}_1,{\mathbf{v}}_2,{\mathbf{v}}_3\}$ es linealmente independiente, demuestre que $\{{\mathbf{v}}_1,{\mathbf{v}}_1+{\mathbf{v}}_2,{\mathbf{v}}_1+{\mathbf{v}}_2+{\mathbf{v}}_3\}$ también es linealmente independiente.

8. Análisis paramétrico: Para qué valores de $h$ el conjunto es linealmente independiente: $\left\{\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right],\left[\begin{array}{c}4\\ 5\\ 6\end{array}\right],\left[\begin{array}{c}2\\ 1\\ h\end{array}\right]\right\}$

9. Implicación: Si $\{{\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_p\}$ es linealmente dependiente, ¿qué puede decir sobre $\{{\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_p,{\mathbf{v}}_{p+1}\}$?

---

🎯 Conceptos Clave para Repasar

Resumen de Conceptos Fundamentales

1. Independencia lineal: Solo la combinación trivial da el vector cero
2. Dependencia lineal: Existe una relación no trivial que da el vector cero
3. Método matricial: Resolver $A\mathbf{x}=0$ donde columnas de $A$ son los vectores
4. Criterio de columnas pivote: Independientes ⟺ todas las columnas son pivote
5. Teorema del tamaño: Más vectores que dimensión ⇒ dependientes
6. Vector cero: Si está en el conjunto ⇒ dependientes
7. Dos vectores: Dependientes ⟺ uno es múltiplo del otro
8. Interpretación geométrica: Independientes ⟺ no coplanares (en la dimensión apropiada)

---

✅ Checklist de Estudio

Lista de Verificación

• Entiendo la definición formal de independencia lineal
• Puedo distinguir entre dependencia e independencia lineal
• Sé usar el método matricial para determinar independencia
• Reconozco cuándo aplicar los teoremas especiales (vector cero, tamaño)
• Puedo encontrar relaciones de dependencia explícitas
• Comprendo la interpretación geométrica
• Relaciono independencia con variables libres
• Identifico columnas pivote y su relación con independencia
• Puedo construir conjuntos independientes y dependientes

---

🔗 Conexiones con Otros Temas

Vínculos Conceptuales

Próximas clases:

• 13) Intro a Transformaciones Lineales: Transformaciones lineales (kernel e inyectividad)
• 22) Espacios y Subespacios Vectoriales: Subespacios vectoriales
• 23) Bases Independencia lineal: Bases y dimensión (conjuntos independientes maximales)

Conceptos relacionados:

• Base - Conjunto independiente que genera un espacio
• Dimension - Número de vectores en una base
• Rango - Número máximo de columnas independientes

---

📚 Referencias

Lectura Principal

• Lay, D. Álgebra Lineal y sus Aplicaciones. Sección 1.7, págs. 55-60

---

🏷️ Tags

algebra-lineal independencia-lineal dependencia-lineal sistemas-homogeneos combinacion-lineal columnas-pivote vectores