5) Introducción a Sistemas de Ecuaciones LinealesAi

📚 Introducción

Esta clase introduce uno de los conceptos fundamentales del álgebra lineal: los sistemas de ecuaciones lineales. Comenzaremos con una perspectiva geométrica que nos permitirá visualizar estos sistemas como intersecciones de planos en el espacio, proporcionando intuición sobre el número y tipo de soluciones posibles.

Objetivos de la Clase

• Representar problemas geométricos de intersección de planos como motivación
• Comprender la interpretación geométrica de sistemas lineales
• Identificar los posibles números de soluciones de un sistema
• Establecer las bases conceptuales para el estudio sistemático de sistemas lineales

---

1. Motivación Geométrica: Intersección de Planos

1.1 El Problema Geométrico

Consideremos el problema de encontrar la intersección de dos planos en el espacio tridimensional ${\mathbb{R}}^3$. Este problema geométrico aparentemente simple nos llevará naturalmente al concepto de sistemas de ecuaciones lineales.

Problema Motivador

Dados dos planos en ${\mathbb{R}}^3$:

• Plano 1: $2x+y-z=3$
• Plano 2: $x-y+2z=1$

¿Cuál es su intersección?

1.2 Interpretación Geométrica

La intersección de dos planos puede resultar en tres casos fundamentales:

Casos de Intersección de Dos Planos

Caso 1: Los planos se intersectan en una línea recta

• Los planos no son paralelos
• Existe una infinidad de puntos de intersección

Caso 2: Los planos son paralelos y distintos

• No hay intersección
• No existen puntos comunes

Caso 3: Los planos son coincidentes

• Todos los puntos del plano son comunes
• Infinitas soluciones

---

2. De la Geometría al Álgebra

2.1 Traducción del Problema

El problema geométrico de encontrar la intersección se traduce algebraicamente en resolver el sistema:

$\{\begin{array}{l}2x+y-z=3\\ x-y+2z=1\end{array}$

Conexión Clave

Cada punto $(x,y,z)$ que satisface ambas ecuaciones simultáneamente representa un punto en la intersección de los dos planos.

2.2 Ejemplo Resuelto

Ejemplo 1 - Intersección de Dos Planos

Problema: Encuentre la intersección de los planos:

• $x+y-z=2$
• $2x-y+z=1$

Solución:

Sumando las ecuaciones: $(x+y-z)+(2x-y+z)=2+1$ $3x=3$ $x=1$

Sustituyendo en la primera ecuación: $1+y-z=2$ $y-z=1$ $y=z+1$

Resultado: La intersección es la línea parametrizada por: $\left(\begin{array}{c}x\\ y\\ z\end{array}\right)=\left(\begin{array}{c}1\\ 1\\ 0\end{array}\right)+t\left(\begin{array}{c}0\\ 1\\ 1\end{array}\right)$

---

3. Extensión a Tres Planos

3.1 Casos Posibles

Cuando consideramos la intersección de tres planos, la variedad de casos aumenta considerablemente:

Casos de Intersección de Tres Planos

1. Un punto único: Los tres planos se intersectan en exactamente un punto

2. Una línea: Los tres planos se intersectan a lo largo de una línea común

3. Un plano: Los tres planos son el mismo (coincidentes)

4. Sin intersección: No existe punto común a los tres planos

5. Casos degenerados: Combinaciones de paralelismo y coincidencia

3.2 Ejemplo con Tres Planos

Ejemplo 2 - Sistema de Tres Ecuaciones

Problema: Analice geométricamente el sistema: $\{\begin{array}{l}x+y+z=6\\ 2x-y+z=3\\ x+2y-z=1\end{array}$

Análisis: Este sistema representa la intersección de tres planos. La solución, si existe y es única, será un punto en ${\mathbb{R}}^3$.

---

4. Generalización y Conceptos Fundamentales

4.1 Sistemas Lineales Generales

Observación Clave

Un sistema de ecuaciones lineales puede interpretarse geométricamente como la intersección de:

• Rectas en ${\mathbb{R}}^2$
• Planos en ${\mathbb{R}}^3$
• Hiperplanos en ${\mathbb{R}}^n$ (para $n>3$)

4.2 Tipos de Soluciones

Basándose en la interpretación geométrica, todo sistema de ecuaciones lineales puede tener:

Teorema - Tipos de Soluciones

Un sistema de ecuaciones lineales tiene exactamente una de las siguientes posibilidades:

1. Solución única: Las entidades geométricas se intersectan en un punto

2. Infinitas soluciones: Las entidades geométricas se intersectan en una línea, plano, etc.

3. Sin solución: Las entidades geométricas no tienen intersección común

4.3 Terminología

Definiciones Fundamentales

Sistema consistente: Tiene al menos una solución

• Puede tener solución única o infinitas soluciones

Sistema inconsistente: No tiene solución

• Las entidades geométricas no se intersectan

---

5. Ejemplos en ${\mathbb{R}}^2$

5.1 Intersección de Rectas

En el plano, un sistema de dos ecuaciones lineales representa la intersección de dos rectas:

Ejemplo 3 - Casos en \mathbb{R}^2

Caso A: Rectas que se intersectan $\{\begin{array}{l}x+y=3\\ x-y=1\end{array}$

Solución: $(2,1)$ - punto único de intersección

Caso B: Rectas paralelas (Pendiente igual, no sobrepuestas) $\{\begin{array}{l}x+y=3\\ x+y=5\end{array}$

Resultado: Sin solución (inconsistente)

Caso C: Rectas coincidentes $\{\begin{array}{l}x+y=3\\ 2x+2y=6\end{array}$

Resultado: Infinitas soluciones

5.2 Visualización Gráfica

---

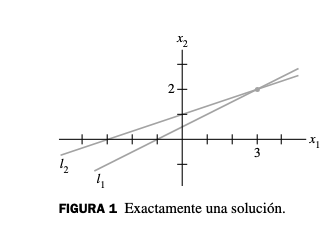
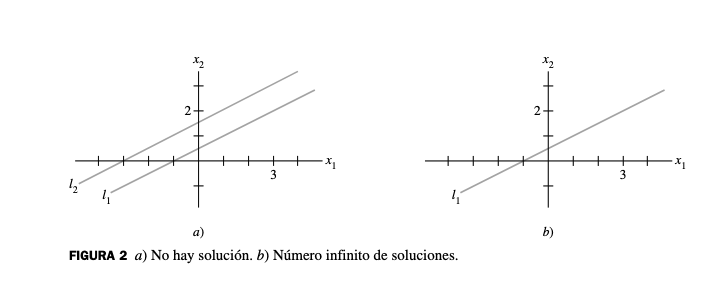
6. Aplicaciones y Motivación

6.1 Problemas de la Vida Real

Aplicaciones Prácticas

Los sistemas de ecuaciones lineales aparecen en:

• Ingeniería: Análisis de circuitos eléctricos
• Economía: Modelos de equilibrio de mercado
• Física: Problemas de equilibrio de fuerzas
• Computación: Procesamiento de imágenes y señales
• Optimización: Programación lineal

---

🚨 Conceptos Clave para Recordar

Ideas Centrales

1. Interpretación geométrica: Los sistemas lineales representan intersecciones de entidades geométricas

2. Tres casos únicos: Todo sistema tiene exactamente una solución, infinitas soluciones, o ninguna solución

3. Consistencia: Un sistema es consistente si tiene solución, inconsistente si no la tiene

4. Dimensión: En ${\mathbb{R}}^n$, trabajamos con intersecciones de hiperplanos de dimensión $n-1$

---

📝 Ejercicios y Problemas

Ejercicios Básicos

Ejercicios de Práctica

1. Análisis geométrico: Para cada sistema, determine geométricamente el tipo de solución:

   a) $\{\begin{array}{l}x+y=4\\ 2x-y=2\end{array}$

   b) $\{\begin{array}{l}x+y=4\\ x+y=7\end{array}$

   c) $\{\begin{array}{l}x+y=4\\ 3x+3y=12\end{array}$

2. Interpretación espacial: Describa geométricamente qué representa cada sistema en ${\mathbb{R}}^3$:

   a) $\{\begin{array}{l}x+y+z=1\\ x-y+z=0\end{array}$

   b) $\{\begin{array}{l}x+y+z=1\\ x+y+z=2\end{array}$

Problemas de Aplicación

Problemas Avanzados

3. Problema de equilibrio: Tres fuerzas actúan sobre un objeto en equilibrio. Si las componentes x de las fuerzas son 2, -1, y 3, y las componentes y son 1, 2, y -2, formule el sistema de ecuaciones que describe el equilibrio.

4. Análisis paramétrico: Para qué valores de $k$ el siguiente sistema tiene:

   • Solución única
   • Infinitas soluciones
   • Sin solución

   $\{\begin{array}{l}x+y=3\\ 2x+ky=6\end{array}$

---

🎯 Preparación para la Próxima Clase

Lo que Viene

En la Clase 06, formalizaremos estas ideas geométricas mediante:

• Definiciones precisas de sistemas lineales
• Conceptos de solución y conjunto solución
• Sistemas equivalentes
• Notación estándar y terminología algebraica

---

🏷️ Tags

algebra-lineal sistemas-ecuaciones-lineales interpretacion-geometrica interseccion-planos consistencia inconsistencia clase-05 motivacion-geometrica

---

📚 Referencias

Lectura Principal

• Lay, D. Álgebra Lineal y sus Aplicaciones. Sección 1.1, págs. 3-7
• Poole, D. Álgebra lineal: Una introducción moderna. Sección 2.1, págs. 68-75