1) Limites de Funciones

Clase 01: Límites de Funciones

📚 Introducción

Esta clase introduce el concepto fundamental de límite, piedra angular del cálculo diferencial e integral. Comprenderemos tanto gráfica como numéricamente qué significa que una función se aproxime a un valor, explorando límites laterales y casos especiales como los límites infinitos.

Objetivos de la Clase

• Comprender gráfica y numéricamente el concepto de límite ${\lim }_{x\to a}f(x)=L$
• Entender la relación con los límites laterales
• Identificar cuándo un límite existe o no existe
• Reconocer límites infinitos y asíntotas verticales

---

1. Concepto de Límite

1.1 Definición Fundamental

Definición - Límite de una Función

Diremos que el Limite-de-una-funcion existe cuando: ${\lim }_{x\to a}f(x)=L$

Esto significa que $f(x)$ se acerca a $L$ cuando $x$ se acerca al número $a$ (sin necesariamente alcanzarlo).

1.2 Interpretación Gráfica

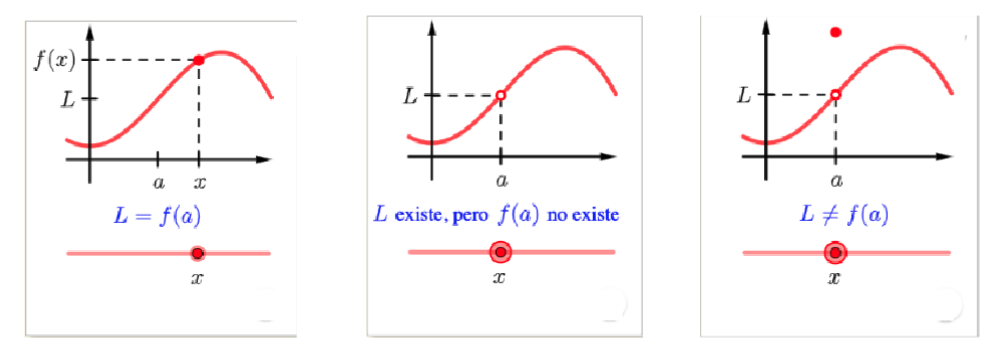
1.3 Características Importantes

• El límite estudia el comportamiento de la función cerca de un punto
• No importa el valor de $f(a)$ (puede no existir)
• Lo importante es el comportamiento cuando $x$ está cerca de $a$, pero $x\ne a$

Observación

El límite puede existir incluso si la función no está definida en el punto $a$

---

2. Ejemplos Fundamentales

2.1 Ejemplo 1: Función Polinómica

Función: $f(x)=x^2-x+2$ cerca de $x=2$

Análisis Numérico

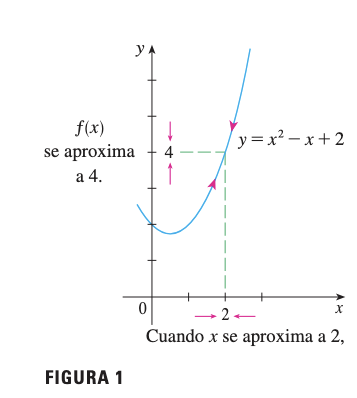
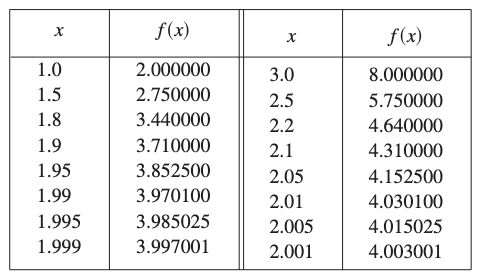
Observación: Cuando $x$ se aproxima a 2 (por ambos lados), $f(x)$ se aproxima a 4.

Conclusión: ${\lim }_{x\to 2}(x^2-x+2)=4$

Interpretación

Podemos hacer que los valores de $f(x)$ estén tan cerca de 4 como queramos, tomando $x$ suficientemente cercano a 2.

2.2 Ejemplo 2: Función Definida por Partes

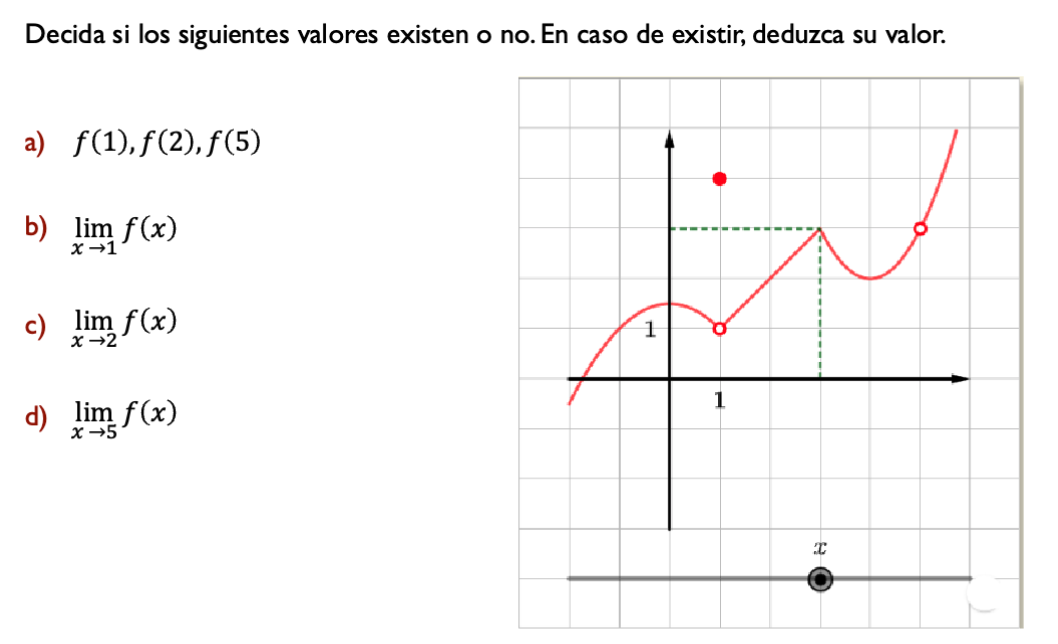
Análisis de la gráfica:

• a) $f(1)=4$, $f(2)=2$, $f(5)$ no existe
• b) ${\lim }_{x\to 1}f(x)=1$
• c) ${\lim }_{x\to 2}f(x)=2$
• d) ${\lim }_{x\to 5}f(x)=5$

Nota Importante

Observa que ${\lim }_{x\to 1}f(x)=1\ne f(1)=4$. El límite y el valor de la función pueden ser diferentes.

2.3 Ejemplo 3: Función con Discontinuidad Removible

Función: $f(x)=\frac{x-1}{x^2-1}$

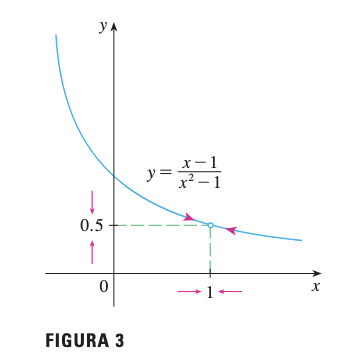
Análisis:

• La función no está definida en $x=1$ (división por cero)
• Sin embargo, podemos analizar el comportamiento cerca de $x=1$
• Simplificando: $\frac{x-1}{x^2-1}=\frac{x-1}{(x-1)(x+1)}=\frac{1}{x+1}$ para $x\ne 1$

Conclusión: ${\lim }_{x\to 1}\frac{x-1}{x^2-1}=0.5$

---

3. Límites Laterales

3.1 Definición de Limites-Laterales

Definición - Límite por la Izquierda

${\lim }_{x\to a^{-}}f(x)=L$

El límite de $f(x)$ cuando $x$ tiende a $a$ por la izquierda es $L$ si podemos hacer que $f(x)$ se acerque arbitrariamente a $L$ tomando valores de $x<a$ suficientemente cercanos a $a$.

Definición - Límite por la Derecha

${\lim }_{x\to a^{+}}f(x)=L$

El límite de $f(x)$ cuando $x$ tiende a $a$ por la derecha es $L$ si podemos hacer que $f(x)$ se acerque arbitrariamente a $L$ tomando valores de $x>a$ suficientemente cercanos a $a$.

3.2 Teorema de Existencia del Límite

Teorema Fundamental El límite existe si y solo si ambos límites laterales existen y son iguales:

${\lim }_{x\to a}f(x)=L\text{si y solo si}{\lim }_{x\to a^{-}}f(x)=L\text{y}{\lim }_{x\to a^{+}}f(x)=L$

3.3 Ejemplo: Función de Heaviside

La Funcion-de-Heaviside $H(t)$ se define como:

$H(t)=\{\begin{array}{llc}0& \text{si }t<01& \text{si }t\ge 0\end{array}$

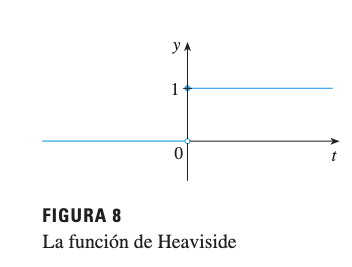
Análisis de límites laterales:

• ${\lim }_{t\to 0^{-}}H(t)=0$ (aproximándose por la izquierda)
• ${\lim }_{t\to 0^{+}}H(t)=1$ (aproximándose por la derecha)

Conclusión: Como los límites laterales son diferentes, ${\lim }_{t\to 0}H(t)$ NO EXISTE.

3.4 Ejemplo: Análisis Gráfico Completo

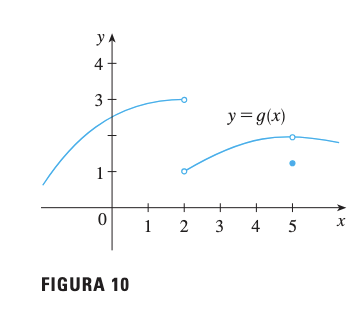
Analizar los siguientes límites de la función $g(x)$:

Límite	Valor	Justificación
a) ${\lim }_{x\to 2^{-}}g(x)$	3	La función se aproxima a 3 por la izquierda
b) ${\lim }_{x\to 2^{+}}g(x)$	5	La función se aproxima a 5 por la derecha
c) ${\lim }_{x\to 2}g(x)$	No existe	$3\ne 5$, límites laterales diferentes
d) ${\lim }_{x\to 5^{-}}g(x)$	2	La función se aproxima a 2 por la izquierda
e) ${\lim }_{x\to 5^{+}}g(x)$	2	La función se aproxima a 2 por la derecha
f) ${\lim }_{x\to 5}g(x)$	2	Ambos límites laterales son iguales

---

4. Límites Infinitos

4.1 Definición de Limites-Infinitos

Definición - Límite Infinito Positivo

${\lim }_{x\to a}f(x)=\infty$

Los valores de $f(x)$ pueden ser arbitrariamente grandes (tan grandes como queramos), tomando $x$ suficientemente cerca de $a$, pero $x\ne a$.

Definición - Límite Infinito Negativo

${\lim }_{x\to a}f(x)=-\infty$

Los valores de $f(x)$ pueden ser negativos arbitrariamente grandes en valor absoluto, tomando $x$ suficientemente cerca de $a$, pero $x\ne a$.

4.2 Límites Infinitos Laterales

Los límites infinitos también pueden analizarse lateralmente:

$$\begin{array}{cc}{\lim }_{x\to a^{-}}f(x)=\infty & {\lim }_{x\to a^{+}}f(x)=\infty \\ {\lim }_{x\to a^{-}}f(x)=-\infty & {\lim }_{x\to a^{+}}f(x)=-\infty \end{array}$$

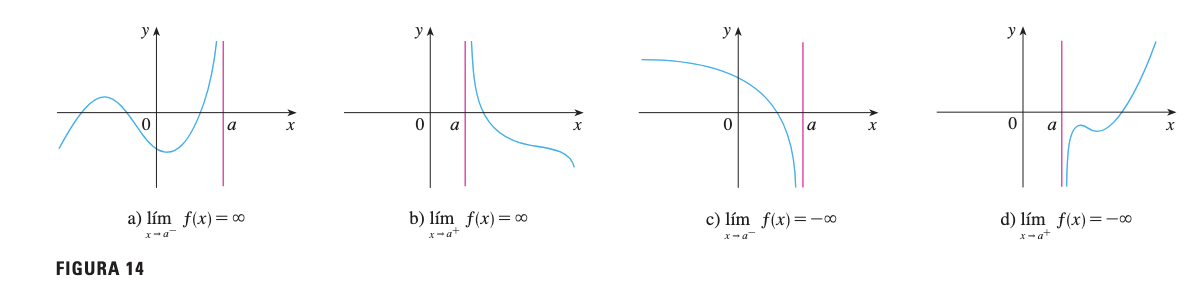
4.3 Asíntotas Verticales

Definición - Asíntota Vertical

La recta $x=a$ es una Asintota-Vertical de la curva $y=f(x)$ si al menos una de las siguientes afirmaciones es verdadera:

$$\begin{array}{ccc}{\lim }_{x\to a^{-}}f(x)=\infty & {\lim }_{x\to a}f(x)=\infty & {\lim }_{x\to a^{+}}f(x)=\infty \\ {\lim }_{x\to a^{-}}f(x)=-\infty & {\lim }_{x\to a}f(x)=-\infty & {\lim }_{x\to a^{+}}f(x)=-\infty \end{array}$$

4.4 Ejemplo: Análisis de $f(x)=\frac{1}{x^2}$

Problema: Encontrar ${\lim }_{x\to 0}\frac{1}{x^2}$

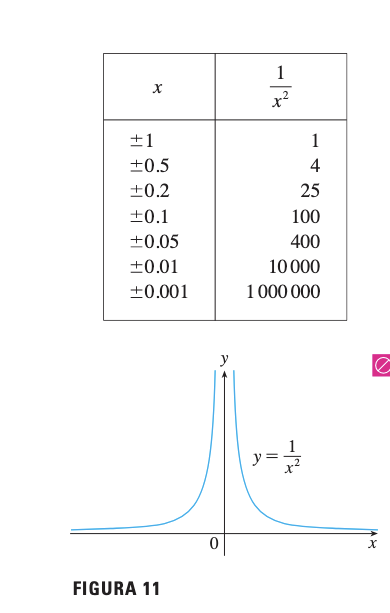
Análisis:

• Conforme $x\to 0$, $x^2\to 0^{+}$ (siempre positivo)
• Por tanto, $\frac{1}{x^2}\to \infty$
• Los valores pueden hacerse arbitrariamente grandes

Conclusión: ${\lim }_{x\to 0}\frac{1}{x^2}=\infty$

Importante

Escribir "$=\infty$" es una notación especial. NO significa que:

• El límite existe
• $\infty$ sea un número

Simplemente describe la forma particular en que el límite no existe: la función crece sin cota.

---

📝 Estrategias para Calcular Límites

Método Gráfico

1. Observar el comportamiento de la función cerca del punto
2. Analizar por separado los límites laterales
3. Verificar si coinciden

Método Numérico

4. Crear tabla de valores acercándose por la izquierda
5. Crear tabla de valores acercándose por la derecha
6. Observar a qué valor convergen

Método Algebraico

7. Simplificar la expresión si es posible
8. Factorizar y cancelar términos comunes
9. Evaluar la expresión simplificada

---

🎯 Conceptos Clave para Repasar

Resumen de Conceptos

1. Límite: Comportamiento de una función al acercarse a un punto
2. Límites laterales: Aproximación por izquierda y derecha
3. Existencia del límite: Requiere igualdad de límites laterales
4. Límites infinitos: Crecimiento sin cota de la función
5. Asíntota vertical: Recta donde la función tiende a infinito
6. Discontinuidad removible: Límite existe pero función no está definida

---

🚨 Errores Comunes

Error 1: Confundir el límite con el valor de la función

• Incorrecto: Asumir que ${\lim }_{x\to a}f(x)=f(a)$
• Correcto: ${\lim }_{x\to a}f(x)$ puede ser diferente de $f(a)$

Error 2: Pensar que \infty es un número

• Incorrecto: Operar con $\infty$ como si fuera un número real
• Correcto: $\infty$ describe un comportamiento, no es un valor

Error 3: Asumir que el límite siempre existe

• Incorrecto: No verificar límites laterales
• Correcto: Verificar siempre que los límites laterales coincidan

---

📚 Referencias

Lectura Principal

• Sección 2.2: Límite de funciones, págs. 87-93

---

✅ Checklist de Estudio

Lista de Verificación

• Puedo identificar límites a partir de gráficas
• Entiendo la diferencia entre límite y valor de la función
• Puedo calcular límites laterales
• Comprendo cuándo un límite no existe
• Entiendo la función de Heaviside como ejemplo clave

---

🏷️ Tags

calculo limites limites-laterales funcion-heaviside continuidad clase