2) Limites Infinitos y Asintotas Verticales

Clase 02: Límites Infinitos y Asíntotas Verticales

📚 Introducción

Esta clase profundiza en el comportamiento no acotado de las funciones, explorando qué sucede cuando los valores de una función crecen sin límite. Los límites infinitos son fundamentales para entender las asíntotas verticales y el comportamiento de funciones racionales, logarítmicas y trigonométricas cerca de puntos críticos.

Objetivos de la Clase

• Comprender gráfica y numéricamente el concepto de límite infinito ${\lim }_{x\to a}f(x)=\infty$
• Relacionar límites infinitos con límites laterales
• Identificar y analizar asíntotas verticales
• Entender que la existencia de la asíntota vertical depende de la explosión de la función

---

1. Límites Infinitos

1.1 Definición de Limites-Infinitos

Definición - Límite Infinito

Positivo Sea $f$ una función definida por ambos lados de $a$, excepto posiblemente en $a$ misma. Entonces: ${\lim }_{x\to a}f(x)=\infty$

Significa que los valores de $f(x)$ pueden ser arbitrariamente grandes (tanto como queramos), tomando $x$ suficientemente cerca de $a$, pero no igual a $a$.

Definición - Límite Infinito Negativo

Sea $f$ una función definida por ambos lados de $a$, excepto posiblemente en $a$ misma. Entonces: ${\lim }_{x\to a}f(x)=-\infty$

Significa que los valores de $f(x)$ pueden ser negativos arbitrariamente grandes en valor absoluto, tomando $x$ suficientemente cerca de $a$, pero no igual a $a$.

1.2 Notación y Lectura

El símbolo ${\lim }_{x\to a}f(x)=-\infty$ se puede leer como:

• “El límite de $f(x)$ cuando $x$ se aproxima a $a$ es infinito negativo”
• “La función $f(x)$ decrece sin cota cuando $x$ tiende a $a$”

Importante sobre la Notación

Escribir "$=\infty$" es una notación especial:

• NO significa que el límite existe
• NO significa que $\infty$ sea un número
• Describe la forma particular en que el límite no existe

1.3 Límites Infinitos Laterales

Los límites infinitos pueden analizarse desde cada lado:

$$\begin{array}{cc}{\lim }_{x\to a^{-}}f(x)=\infty & {\lim }_{x\to a^{+}}f(x)=\infty \\ {\lim }_{x\to a^{-}}f(x)=-\infty & {\lim }_{x\to a^{+}}f(x)=-\infty \end{array}$$

Recordatorio

• $x\to a^{-}$: Se consideran solo valores de $x$ menores que $a$
• $x\to a^{+}$: Se consideran solo valores de $x$ mayores que $a$

1.4 Casos Posibles de Comportamiento

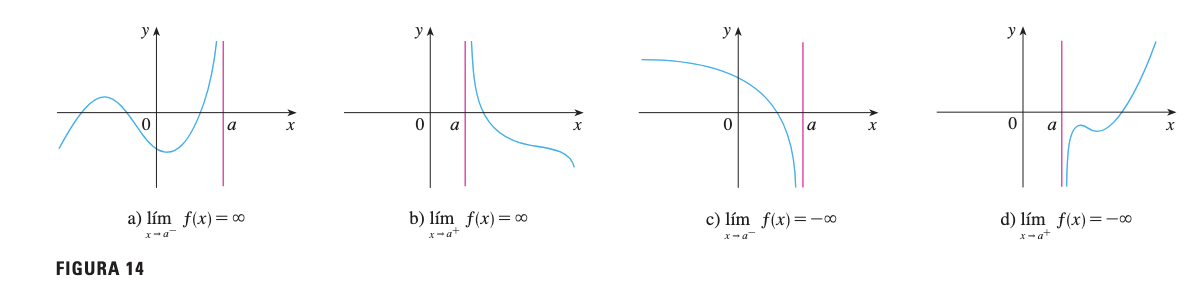
La figura muestra cuatro casos típicos de límites infinitos y sus combinaciones laterales.

---

2. Asíntotas Verticales

2.1 Definición de Asintota-Vertical

Definición - Asíntota Vertical

La recta $x=a$ se llama asíntota vertical de la curva $y=f(x)$ si al menos una de las siguientes afirmaciones es verdadera:

$$\begin{array}{ccc}{\lim }_{x\to a^{-}}f(x)=\infty & {\lim }_{x\to a}f(x)=\infty & {\lim }_{x\to a^{+}}f(x)=\infty \\ {\lim }_{x\to a^{-}}f(x)=-\infty & {\lim }_{x\to a}f(x)=-\infty & {\lim }_{x\to a^{+}}f(x)=-\infty \end{array}$$

2.2 Interpretación Geométrica

Una asíntota vertical representa una recta a la cual la gráfica de la función se acerca indefinidamente sin tocarla, con los valores de la función creciendo o decreciendo sin cota.

Observación Clave

La existencia de una asíntota vertical depende de la “explosión” de la función por alguno de los lados de la asíntota.

---

3. Ejemplos Fundamentales

3.1 Ejemplo Básico: $f(x)=\frac{1}{x^2}$

Problema: Encontrar ${\lim }_{x\to 0}\frac{1}{x^2}$

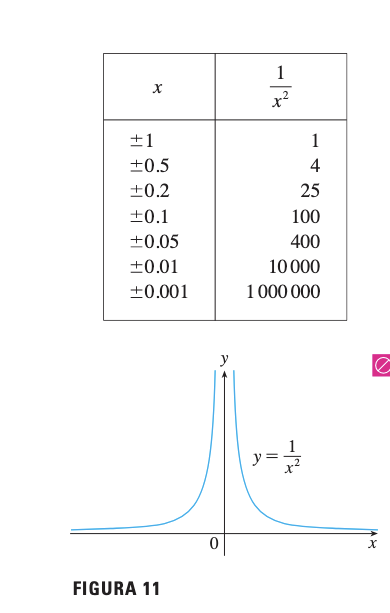
Análisis:

• Conforme $x\to 0$, $x^2\to 0^{+}$ (siempre positivo)
• Por tanto, $\frac{1}{x^2}\to \infty$
• Los valores de $f(x)$ pueden hacerse arbitrariamente grandes

Conclusión: ${\lim }_{x\to 0}\frac{1}{x^2}=\infty$

Por lo tanto, $x=0$ es una asíntota vertical.

3.2 Ejemplo: Función Racional con Límites Laterales Diferentes

Problema: Encontrar ${\lim }_{x\to 3^{+}}\frac{2x}{x-3}$ y ${\lim }_{x\to 3^{-}}\frac{2x}{x-3}$

Solución:

Análisis por la derecha

($x\to 3^{+}$)

• Si $x>3$: $x-3>0$ (positivo pequeño)
• $2x\approx 6$ (positivo)
• Cociente: $\frac{2x}{x-3}\to +\infty$

${\lim }_{x\to 3^{+}}\frac{2x}{x-3}=\infty$

Análisis por la izquierda

($x\to 3^{-}$)

• Si $x<3$: $x-3<0$ (negativo pequeño)
• $2x\approx 6$ (positivo)
• Cociente: $\frac{2x}{x-3}\to -\infty$

${\lim }_{x\to 3^{-}}\frac{2x}{x-3}=-\infty$

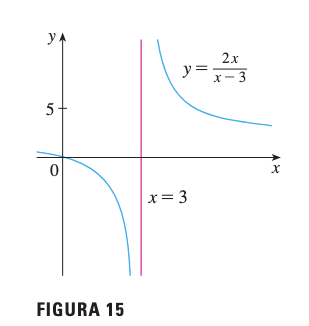
Conclusión: La recta $x=3$ es una asíntota vertical.

3.3 Ejemplo: Función Tangente

Problema: Encontrar las asíntotas verticales de $f(x)=\tan x$

Solución:

Como $\tan x=\frac{\sin x}{\cos x}$, hay posibles asíntotas verticales donde $\cos x=0$.

Análisis

en $x=\pi /2$

• $\cos x\to 0^{+}$ cuando $x\to (\pi /2{)}^{-}$
• $\cos x\to 0^{-}$ cuando $x\to (\pi /2{)}^{+}$
• $\sin x>0$ cerca de $\pi /2$

Por lo tanto: ${\lim }_{x\to (\pi /2{)}^{-}}\tan x=\infty \text{y}{\lim }_{x\to (\pi /2{)}^{+}}\tan x=-\infty$

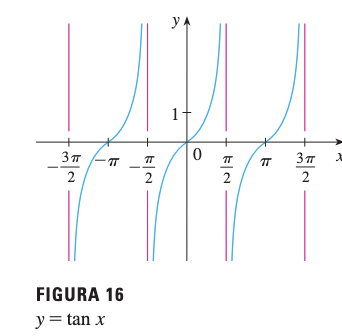
Conclusión: Las rectas $x=\frac{(2n+1)\pi }{2}$, donde $n\in \mathbb{Z}$, son todas asíntotas verticales.

3.4 Ejemplo: Logaritmo Natural

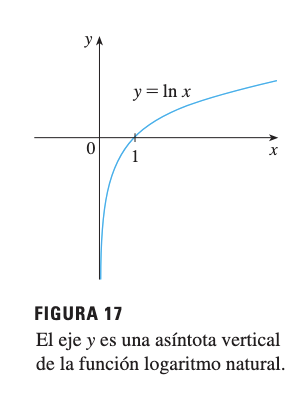
Función Logaritmo Natural

La función Logaritmo-Natural $y=\ln x$ tiene una asíntota vertical en $x=0$: ${\lim }_{x\to 0^{+}}\ln x=-\infty$

Por lo tanto, el eje $y$ (la recta $x=0$) es una asíntota vertical.

---

4. Estrategias para Identificar Asíntotas Verticales

Método Algebraico

1. Funciones racionales: Buscar valores donde el denominador es cero
2. Verificar que el numerador no sea cero en ese punto
3. Analizar el signo del cociente por ambos lados
4. Determinar si el límite es $+\infty$ o $-\infty$

Método Gráfico

1. Identificar puntos donde la gráfica parece “explotar”
2. Observar el comportamiento por ambos lados
3. Verificar si la función crece o decrece sin cota
4. Trazar la línea vertical correspondiente

Funciones Especiales

• Logarítmicas: Asíntota en $x=0$ para $\ln x$ y $\log x$
• Trigonométricas:
  • $\tan x$: en $x=\frac{(2n+1)\pi }{2}$
  • $\sec x$: en $x=\frac{(2n+1)\pi }{2}$
  • $\csc x$: en $x=n\pi$
• Racionales: Donde el denominador es cero y el numerador no

---

5. Relación entre Límites Infinitos y Comportamiento de la Función

5.1 Interpretación del Signo

Teorema del Signo

Para $f(x)=\frac{g(x)}{h(x)}$ cerca de $x=a$ donde $h(a)=0$ y $g(a)\ne 0$:

Signo de $g(x)$	Signo de $h(x)$	Límite
$+$	$0^{+}$	$+\infty$
$+$	$0^{-}$	$-\infty$
$-$	$0^{+}$	$-\infty$
$-$	$0^{-}$	$+\infty$

5.2 Casos Especiales

Formas Indeterminadas

Si tanto el numerador como el denominador tienden a cero, es decir una indeterminación tipo $\frac{0}{0}$ NO podemos concluir directamente sobre el límite. Estos casos requieren técnicas adicionales como:

• Factorización
• Racionalización
• Regla de L’Hôpital (tema posterior)

---

🎯 Conceptos Clave para Repasar

Resumen de Conceptos

1. Límite infinito: Comportamiento no acotado de una función
2. Asíntota vertical: Recta donde la función “explota”
3. Análisis lateral: Los límites infinitos pueden diferir por cada lado
4. Notación especial: $\infty$ describe comportamiento, no es un número
5. Identificación: Buscar donde denominadores se anulan
6. Funciones especiales: Cada tipo tiene sus asíntotas características

---

🚨 Errores Comunes

Error 1: Tratar \infty como un número

• Incorrecto: Operar algebraicamente con $\infty$
• Correcto: Usar $\infty$ solo para describir comportamiento no acotado

Error 2: No verificar límites laterales

• Incorrecto: Asumir que si hay asíntota, ambos lados van al mismo infinito
• Correcto: Los límites laterales pueden ser diferentes ($+\infty$ vs $-\infty$)

Error 3: Confundir límite infinito con límite no existente

• Incorrecto: Decir que el límite existe cuando es infinito
• Correcto: El límite infinito es una forma específica de no existencia

Error 4: Olvidar verificar el numerador

• Incorrecto: Toda división por cero produce asíntota vertical
• Correcto: Si numerador y denominador son cero, puede no haber asíntota

---

📝 Ejercicios Propuestos

Ejercicios de Práctica

1. Encontrar las asíntotas verticales de $f(x)=\frac{x^2-1}{x^2-4}$
2. Analizar ${\lim }_{x\to 2^{\pm }}\frac{3x+1}{(x-2{)}^2}$
3. Determinar las asíntotas de $g(x)=\frac{\ln (x+1)}{x}$
4. Estudiar el comportamiento de $h(x)=\cot x$ cerca de sus asíntotas

---

📚 Referencias

Lectura Principal

• Sección 2.2: Límite de funciones, págs. 93-95

---

Sugerencia de Estudio

Lo mismo que la clase anterior. Enfatizar que la existencia de la asíntota vertical depende de la explosión de la función por alguno de los lados de la asíntota y no necesariamente por ambos. Enfatizar que en estos casos se determina el límite, pero al no ser un número real el límite no existe.

Es un buen momento para enfatizar la importancia de las definiciones.

---

✅ Checklist de Estudio

Lista de Verificación

• Comprendo qué significa un límite infinito
• Puedo identificar asíntotas verticales algebraicamente
• Entiendo la diferencia entre $+\infty$ y $-\infty$ en límites laterales
• Puedo analizar funciones racionales cerca de puntos críticos
• Reconozco las asíntotas de funciones trigonométricas básicas
• Entiendo que $\infty$ no es un número sino una descripción
• Puedo relacionar el signo de numerador y denominador con el límite
• Comprendo la diferencia entre límite infinito y forma indeterminada

---

🏷️ Tags

calculo limites limites-infinitos asintotas-verticales funciones-racionales funciones-trigonometricas logaritmo-natural comportamiento-asintotico clase-02 clase