6) Continuidad en Un Punto

Clase 06: Continuidad en un Punto

📚 Introducción

Esta clase introduce el concepto fundamental de continuidad, que formaliza matemáticamente la idea intuitiva de una función “sin saltos” o “sin interrupciones”. La continuidad es esencial para entender el comportamiento de las funciones y es prerrequisito para conceptos más avanzados como la derivabilidad y la integrabilidad.

Objetivos de la Clase

• Determinar si una función es continua o discontinua en un número
• Clasificar tipos de discontinuidad: removible y discontinuidad no removible o esencial
• Comprender la continuidad en un intervalo
• Aplicar teoremas sobre continuidad de operaciones con funciones

---

1. Definición de Continuidad

1.1 Continuidad en un Punto

Definición - Continuidad en un Punto

Una función $f$ es continua en un número $x=a$ si: ${\lim }_{x\to a}f(x)=f(a)$

Esta definición requiere que se cumplan tres condiciones:

1. $f(a)$ está definida (es decir, $a\in \text{Dom}(f)$)
2. ${\lim }_{x\to a}f(x)$ existe
3. ${\lim }_{x\to a}f(x)=f(a)$

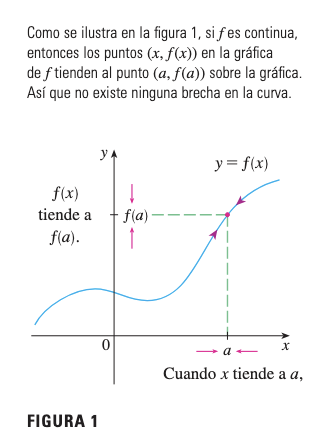
Interpretación Intuitiva

En funciones continuas, un pequeño cambio en $x$ implica un pequeño cambio en $f(x)$. Geométricamente, la gráfica puede dibujarse sin levantar la pluma del papel.

1.2 Continuidad Lateral

Definición - Continuidad por la Derecha

Una función $f$ es continua por la derecha en un número $x=a$ si: ${\lim }_{x\to a^{+}}f(x)=f(a)$

Definición - Continuidad por la Izquierda

Una función $f$ es continua por la izquierda en un número $x=a$ si: ${\lim }_{x\to a^{-}}f(x)=f(a)$

1.3 Continuidad sobre un Intervalo

Definición - Continuidad en un Intervalo

Una función $f$ es continua sobre un intervalo si es continua en cada número en el intervalo.

Si $f$ está definida solo en un lado de un punto extremo del intervalo, entendemos por continua en el punto extremo como continua por la derecha o continua por la izquierda.

Note

Cómo demostrar continuidad sobre un intervalo

Para demostrar que una función $f(x)$ es continua en un intervalo, debes seguir estos pasos:

1. Identificar el tipo de intervalo
   • Intervalo abierto $(a,b)$
   • Intervalo cerrado $[a,b]$
   • Intervalo semiabierto $[a,b)$ o $(a,b]$
2. Para cada punto interior del intervalo
   • Verificar que $f(a)$ está definida
   • Calcular $\underset{x\to a}{\lim }f(x)$
   • Comprobar que $\underset{x\to a}{\lim }f(x)=f(a)$
3. Para los extremos del intervalo (si están incluidos)
   • Extremo izquierdo $a$: Verificar continuidad por la derecha
     • $\underset{x\to a^{+}}{\lim }f(x)=f(a)$
   • Extremo derecho $b$: Verificar continuidad por la izquierda
     • $\underset{x\to b^{-}}{\lim }f(x)=f(b)$
4. Usar teoremas de continuidad
   • Funciones elementales (polinomios, trigonométricas, exponenciales) son continuas en sus dominios
   • Suma, resta, producto y cociente de funciones continuas son continuas
   • Composición de funciones continuas es continua
5. Identificar posibles puntos problemáticos
   • Puntos donde la función cambia de definición
   • Puntos donde hay denominadores que se anulan
   • Puntos de discontinuidad aparente

---

2. Discontinuidades

2.1 Definición de Discontinuidad

Definición - Discontinuidad

Si $f$ está definida cerca de $a$ (en un intervalo abierto que contiene a $a$, excepto quizás en $a$), decimos que $f$ es discontinua en $a$ (o $f$ tiene una discontinuidad en $a$) si $f$ no es continua en $a$.

Interpretación Geométrica

Geométricamente, una función continua en cada número de un intervalo puede pensarse como una función cuya gráfica no tiene interrupciones. La gráfica puede dibujarse sin levantar la pluma del papel.

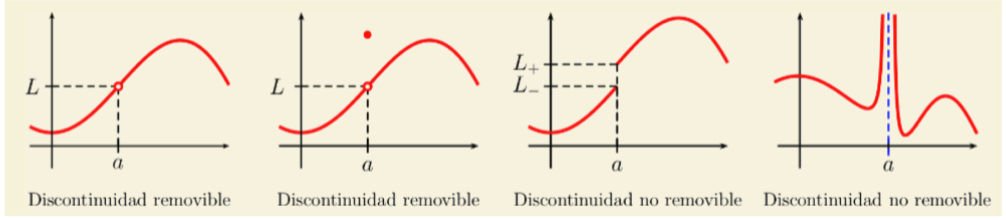
2.2 Clasificación de Discontinuidades

Tipos de Discontinuidades Sea f discontinua en x = a:

1. Discontinuidad Removible: Si ${\lim }_{x\to a}f(x)$ existe
   • Se puede “remover” redefiniendo $f$ solo en $x=a$
2. Discontinuidad No Removible (Esencial): Si ${\lim }_{x\to a}f(x)$ no existe
   • Incluye discontinuidades infinitas y de salto

---

3. Ejemplos de Análisis de Continuidad

3.1 Ejercicio: Identificación Visual

Problema: ¿Para qué valores de $x=a$, $f$ es discontinua?

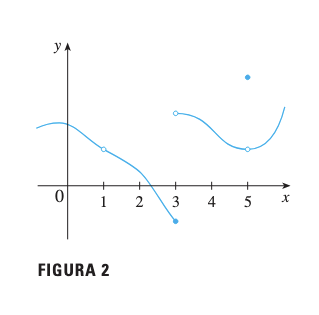
Análisis de la Gráfica Observando la gráfica, f es discontinua en:

• $x=1$: No está definida
• $x=2$: El límite no existe (límites laterales diferentes)
• $x=3$: Está definida y el límite existe, pero ${\lim }_{x\to 3}f(x)\ne f(3)$
• $x=5$: Está definida y el límite existe, pero ${\lim }_{x\to 5}f(x)\ne f(5)$

3.2 Ejemplos con Fórmulas

Analizar continuidad de las siguientes funciones:

a) $f(x)=\frac{x^2-x-2}{x-2}$

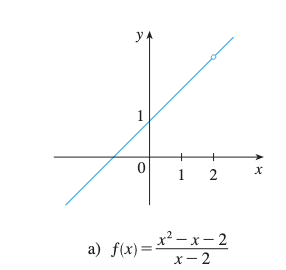
Solución

• $f(2)$ no está definida, así que $f$ es discontinua en $x=2$
• Sin embargo: ${\lim }_{x\to 2}\frac{x^2-x-2}{x-2}={\lim }_{x\to 2}\frac{(x-2)(x+1)}{x-2}={\lim }_{x\to 2}(x+1)=3$
• Conclusión: Discontinuidad removible en $x=2$

b) $f(x)=\{\begin{array}{ll}\frac{1}{x^2},& \text{si }x\ne 0\\ 1,& \text{si }x=0\end{array}$

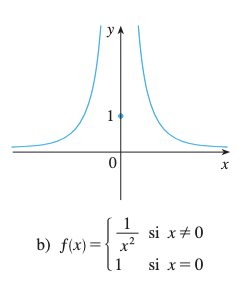
Solución

• $f(0)=1$ está definida
• ${\lim }_{x\to 0}\frac{1}{x^2}=\infty$ (no existe)
• Conclusión: Discontinuidad no removible en $x=0$

c) $f(x)=\{\begin{array}{ll}\frac{x^2-x-2}{x-2},& \text{si }x\ne 2\\ 1,& \text{si }x=2\end{array}$

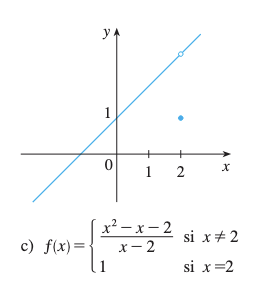
Solución

• $f(2)=1$ está definida
• ${\lim }_{x\to 2}\frac{x^2-x-2}{x-2}=3$ (del inciso a)
• Como ${\lim }_{x\to 2}f(x)=3\ne 1=f(2)$
• Conclusión: Discontinuidad removible en $x=2$

d) $f(x)=\lfloor x\rfloor$ (Función entero mayor)

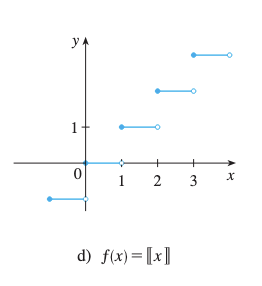
Solución

• En cada entero $n$:
  • $\underset{x\to n^{+}}{\lim }\lfloor x\rfloor =n=f(n)$
  • $\underset{x\to n^{-}}{\lim }\lfloor x\rfloor =n-1\ne f(n)$
• Conclusión: Discontinuidad no removible (de salto) en cada entero

---

4. Ejemplo Importante: Continuidad en un Intervalo

4.1 Función en Intervalo Cerrado

Problema: Demuestre que $f(x)=\sqrt{1-x^2}$ es continua sobre el intervalo $[-1,1]$.

Demostración

Para $-1<a<1$: ${\lim }_{x\to a}f(x)={\lim }_{x\to a}\sqrt{1-x^2}=\sqrt{1-a^2}=f(a)$ Por definición 1, $f$ es continua en $x=a$.

En $x=-1$: ${\lim }_{x\to (-1{)}^{+}}f(x)=\sqrt{1-1}=0=f(-1)$ Por lo tanto, $f$ es continua por la derecha en $x=-1$.

En $x=1$: ${\lim }_{x\to 1^{-}}f(x)=\sqrt{1-1}=0=f(1)$ Por lo tanto, $f$ es continua por la izquierda en $x=1$.

Conclusión: $f$ es continua en $[-1,1]$.

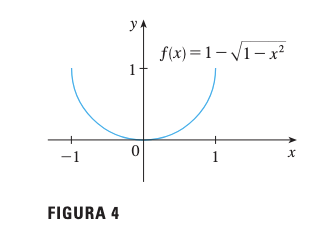
Interpretación Geométrica

La gráfica de $f$ es la mitad inferior de la circunferencia $x^2+y^2=1$.

---

5. Teoremas sobre Continuidad

5.1 Operaciones con Funciones Continuas

Teorema - Álgebra de Funciones Continuas

Si $f$ y $g$ son continuas en $x=a$ y $c\in \mathbb{R}$, entonces las siguientes funciones son también continuas en $x=a$:

1. $f+g$ (suma)
2. $f-g$ (diferencia)
3. $cf$ (múltiplo escalar)
4. $fg$ (producto)
5. $\frac{f}{g}$ si $g(a)\ne 0$ (cociente)

Demostración del Teorema

Cada parte se sigue de las correspondientes leyes de los límites. Por ejemplo, para la suma: ${\lim }_{x\to a}(f+g)(x)={\lim }_{x\to a}f(x)+{\lim }_{x\to a}g(x)=f(a)+g(a)=(f+g)(a)$

5.2 Tipos de Funciones Continuas

Funciones Elementales Continuas

Las siguientes funciones son continuas en su dominio:

• Polinomios: Continuos en todo $\mathbb{R}$
• Funciones racionales: Continuas donde el denominador no es cero
• Funciones raíz: $\sqrt[n]{x}$ continua en su dominio
• Funciones trigonométricas: sen, cos, tan (en su dominio)
• Funciones exponenciales y logarítmicas: En su dominio

---

6. Estrategias para Analizar Continuidad

Método 1: Verificación Directa

1. Verificar que $f(a)$ esté definida
2. Calcular ${\lim }_{x\to a}f(x)$
3. Comprobar que ${\lim }_{x\to a}f(x)=f(a)$

Método 2: Para Funciones Definidas por Partes

1. Analizar continuidad en el interior de cada parte
2. Verificar continuidad en los puntos de transición
3. Calcular límites laterales en puntos de transición

Método 3: Usar Teoremas

1. Identificar funciones elementales continuas
2. Aplicar teoremas sobre operaciones
3. Determinar el dominio de continuidad

---

🎯 Conceptos Clave para Repasar

Resumen de Conceptos

1. Continuidad en un punto: Requiere tres condiciones
2. Discontinuidad removible: El límite existe pero difiere del valor
3. Discontinuidad esencial: El límite no existe
4. Continuidad lateral: Por derecha o izquierda
5. Continuidad en intervalos: En cada punto del intervalo
6. Operaciones continuas: Suma, producto, cociente (con restricciones)

---

🚨 Errores Comunes

Error 1: Confundir existencia del límite con continuidad

• Incorrecto: Si el límite existe, la función es continua
• Correcto: También debe cumplirse que ${\lim }_{x\to a}f(x)=f(a)$

Error 2: No verificar que f(a) esté definida

• Incorrecto: Solo calcular el límite
• Correcto: Verificar las tres condiciones de continuidad

Error 3: Ignorar continuidad lateral en extremos

• Incorrecto: Aplicar continuidad bilateral en extremos de intervalo
• Correcto: Usar continuidad lateral en puntos extremos

---

📝 Ejercicios Propuestos

Ejercicios de Práctica

1. Determinar y clasificar las discontinuidades de $f(x)=\frac{x^2-4}{x^2-3x+2}$
2. Encontrar el valor de $k$ para que $f(x)=\{\begin{array}{llc}{x}^2+k& x<23x-1& x\ge 2\end{array}$ sea continua
3. Demostrar que $f(x)=|x|$ es continua en todo $\mathbb{R}$
4. Analizar la continuidad de $f(x)=\frac{\sin x}{x}$ extendida con $f(0)=1$

---

📚 Referencias

Lectura Principal

• Sección 2.5: Continuidad, págs. 118-121

Sugerencias de Estudio

• Considerar el Ejemplo 2 de la pág. 119
• Importante: en esta clase los estudiantes determinan continuidad/discontinuidad en un punto y no en un intervalo
• La continuidad en un intervalo se abordará en la próxima clase

---

✅ Checklist de Estudio

Lista de Verificación

• Puedo verificar las tres condiciones de continuidad
• Identifico discontinuidades removibles y no removibles
• Comprendo la continuidad lateral
• Puedo analizar funciones definidas por partes
• Aplico teoremas sobre operaciones continuas
• Reconozco funciones elementales continuas
• Distingo entre límite existente y continuidad

---

🏷️ Tags

calculo continuidad discontinuidad discontinuidad-removible discontinuidad-esencial continuidad-lateral teoremas-continuidad clase-06 clase