10) Recta Tangente, Velocidad y el Concepto de Derivada

Clase 10: Recta Tangente, Velocidad y el Concepto de Derivada

📚 Introducción

Esta clase marca el inicio del estudio de las derivadas, uno de los conceptos fundamentales del cálculo. La derivada surge naturalmente al estudiar dos problemas clásicos: encontrar la recta tangente a una curva y determinar la velocidad instantánea de un objeto en movimiento. Ambos problemas conducen al mismo tipo de límite, revelando la profunda conexión entre geometría y física a través del cálculo.

Objetivos de la Clase

• Determinar la recta tangente a la gráfica de una función en un punto dado
• Calcular la velocidad de un objeto que se mueve a lo largo de una línea recta
• Relacionar el concepto de derivada con la pendiente de la recta tangente
• Comprender la derivada como razón de cambio instantánea
• Interpretar geométrica y físicamente el significado de la derivada

---

1. El Problema de la Recta Tangente

1.1 Definición Intuitiva de Recta-Tangente

Definición - Recta Tangente (Enfoque Intuitivo)

La recta tangente a una curva en un punto es la recta que “apenas toca” la curva en ese punto, siguiendo la misma dirección que la curva en ese instante.

1.2 De la Recta Secante a la Recta Tangente

Si tenemos una curva $C$ con ecuación $y=f(x)$ y queremos hallar la recta tangente en el punto $P(a,f(a))$, consideramos un punto cercano $Q(x,f(x))$ donde $x\ne a$.

Recta Secante $PQ$: La pendiente de esta recta es $m_{PQ}=\frac{f(x)-f(a)}{x-a}$

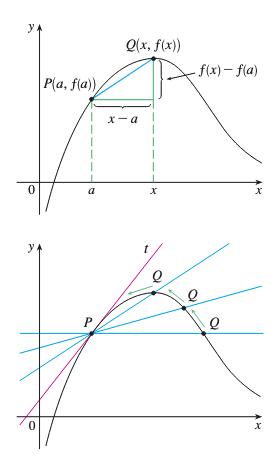
Intuición Geométrica

Cuando $Q$ se acerca a $P$ a lo largo de la curva (es decir, cuando $x\to a$), la recta secante $PQ$ se aproxima a la recta tangente en $P$.

1.3 Definición Formal de Recta Tangente

Definición - Recta Tangente

La recta tangente a la curva $y=f(x)$ en el punto $P(a,f(a))$ es la recta que pasa por $P$ con pendiente

$m={\lim }_{x\to a}\frac{f(x)-f(a)}{x-a}$

siempre que este límite exista.

Ecuación de la Recta Tangente

Si $y=f(x)$ es una curva y la pendiente de su tangente en $(a,f(a))$ es $m=f^{\prime }(a)$, entonces la ecuación de la recta tangente es:

$y-f(a)=f^{\prime }(a)(x-a)$

1.4 Forma Alternativa del Límite

Si escribimos $h=x-a$, entonces $x=a+h$ y cuando $x\to a$ tenemos que $h\to 0$. Por lo tanto:

$m={\lim }_{h\to 0}\frac{f(a+h)-f(a)}{h}$

---

2. Ejemplos de Rectas Tangentes

2.1 Ejemplo 1: Parábola $y=x^2$

Problema: Encuentre la ecuación de la recta tangente a la parábola $y=x^2$ en el punto $(1,1)$.

Solución

En este caso, $a=1$ y $f(x)=x^2$, así que $f(1)=1$.

Paso 1: Calcular la pendiente usando la definición $m={\lim }_{x\to 1}\frac{f(x)-f(1)}{x-1}={\lim }_{x\to 1}\frac{x^2-1}{x-1}$

Paso 2: Simplificar algebraicamente $={\lim }_{x\to 1}\frac{(x-1)(x+1)}{x-1}={\lim }_{x\to 1}(x+1)=2$

Paso 3: Escribir la ecuación de la tangente $y-1=2(x-1)$ $y=2x-1$

2.2 Ejemplo 2: Hipérbola $y=3/x$

Problema: Encuentre una ecuación de la recta tangente a la hipérbola $y=3/x$ en el punto $(3,1)$.

Solución

Sea $f(x)=3/x$. Entonces la pendiente de la tangente en $(3,1)$ es:

$m={\lim }_{h\to 0}\frac{f(3+h)-f(3)}{h}={\lim }_{h\to 0}\frac{\frac{3}{3+h}-1}{h}$

Simplificando: $={\lim }_{h\to 0}\frac{\frac{3-(3+h)}{3+h}}{h}={\lim }_{h\to 0}\frac{-h}{h(3+h)}={\lim }_{h\to 0}\frac{-1}{3+h}=-\frac{1}{3}$

Por lo tanto, la ecuación de la tangente es: $y-1=-\frac{1}{3}(x-3)\text{o bien}y=-\frac{1}{3}x+2$

---

3. El Problema de la Velocidad

3.1 Contexto Físico

En la sección 2.1 investigamos el movimiento de una pelota que cae desde la Torre CN, definiendo su velocidad como el límite de las velocidades promedio.

Situación General

Suponga que un objeto se mueve a lo largo de una línea recta según una ecuación de movimiento $s=f(t)$, donde:

• $s$ = desplazamiento (distancia dirigida) desde el origen
• $t$ = tiempo
• $f$ = función posición del objeto

3.2 Velocidad Promedio vs Velocidad Instantánea

Velocidad Promedio: En el intervalo de tiempo $[a,a+h]$:

$v_{\text{prom}}=\frac{\text{desplazamiento}}{\text{tiempo}}=\frac{f(a+h)-f(a)}{h}$

Definición - Velocidad Instantánea

La velocidad instantánea $v(a)$ en el tiempo $t=a$ es:

$v(a)={\lim }_{h\to 0}\frac{f(a+h)-f(a)}{h}$

Observación Clave

La velocidad es la derivada de la posición:

• Si $r(t)$ es la posición de un objeto en el instante $t$ que se mueve sobre una línea recta
• Entonces su velocidad $v(t)$ está dada por $v(t)=r^{\prime }(t)$
• La derivada es la velocidad del objeto

3.3 Ejemplo 3: Pelota que Cae

Problema: Suponga que se deja caer una pelota desde la plataforma superior de observación de la Torre CN, a 450 m sobre el suelo.

a) ¿Cuál es la velocidad después de 5 s? b) ¿Con qué rapidez cae cuando choca contra el suelo?

Solución

Usando la ecuación de movimiento $s=f(t)=4.9t^2$ (donde $s$ se mide en metros y $t$ en segundos):

Parte a): Calcular $v(5)$

$v(a)={\lim }_{h\to 0}\frac{f(a+h)-f(a)}{h}={\lim }_{h\to 0}\frac{4.9(a+h{)}^2-4.9a^2}{h}$

$={\lim }_{h\to 0}\frac{4.9(a^2+2ah+h^2-a^2)}{h}={\lim }_{h\to 0}\frac{4.9(2ah+h^2)}{h}$

$={\lim }_{h\to 0}4.9(2a+h)=9.8a$

Por lo tanto, $v(5)=(9.8)(5)=49$ m/s

Parte b): Primero encontrar cuándo choca

La pelota choca cuando $s(t_1)=450$: $4.9t_1^2=450⟹t_1=\sqrt{\frac{450}{4.9}}\approx 9.6\text{ s}$

La velocidad al chocar es: $v(t_1)=9.8t_1=9.8\sqrt{\frac{450}{4.9}}\approx 94\text{ m/s}$

---

4. Derivadas

4.1 El Concepto Unificador

Hemos visto que en la búsqueda de:

• La pendiente de una recta tangente (ecuación 2)
• La velocidad de un objeto (ecuación 3)

Surge el mismo tipo de límite:

${\lim }_{h\to 0}\frac{f(a+h)-f(a)}{h}$

Definición - Derivada en un Punto

La derivada de una función $f$ en un número $a$, denotada por $f^{\prime }(a)$ (se lee “f prima de a”), es:

$f^{\prime }(a)={\lim }_{h\to 0}\frac{f(a+h)-f(a)}{h}$

si este límite existe.

4.2 Forma Alternativa

Si escribimos $x=a+h$, entonces $h=x-a$ y cuando $h\to 0$ tenemos $x\to a$:

$f^{\prime }(a)={\lim }_{x\to a}\frac{f(x)-f(a)}{x-a}$

4.3 Interpretaciones de la Derivada

Interpretación Geométrica

La derivada es la pendiente de la recta tangente

Si $y=f(x)$ corresponde a una curva en el plano, entonces su recta tangente en el punto $(a,f(a))$ está dada por: $y-f(a)=f^{\prime }(a)(x-a)$

siendo $f^{\prime }(a)$ la pendiente de la recta tangente.

Interpretación Física

La derivada es la velocidad del objeto

Si $r(t)$ corresponde a la posición de un objeto en el instante de tiempo $t$, que se mueve sobre una línea recta, entonces su velocidad $v(t)$ está dada por: $v(t)=r^{\prime }(t)$

4.4 Ejemplo 4: Cálculo Directo de Derivada

Problema: Encuentre la derivada de la función $f(x)=x^2-8x+9$ en el número $a$.

Solución

$f^{\prime }(a)={\lim }_{h\to 0}\frac{f(a+h)-f(a)}{h}$

$={\lim }_{h\to 0}\frac{[(a+h{)}^2-8(a+h)+9]-[a^2-8a+9]}{h}$

$={\lim }_{h\to 0}\frac{a^2+2ah+h^2-8a-8h+9-a^2+8a-9}{h}$

$={\lim }_{h\to 0}\frac{2ah+h^2-8h}{h}={\lim }_{h\to 0}(2a+h-8)=2a-8$

---

🎯 Conceptos Clave para Repasar

Resumen de Conceptos

1. Recta tangente: Recta que toca la curva siguiendo su dirección en un punto
2. Recta secante: Aproximación a la tangente mediante dos puntos cercanos
3. Velocidad promedio: Desplazamiento dividido por tiempo transcurrido
4. Velocidad instantánea: Límite de velocidades promedio cuando $h\to 0$
5. Derivada: Concepto unificador que representa pendiente y velocidad
6. $f^{\prime }(a)$: Notación para la derivada de $f$ en el punto $a$

---

🚨 Errores Comunes

Error 1: Confundir recta tangente con recta secante

• Incorrecto: Usar dos puntos arbitrarios para definir la tangente
• Correcto: La tangente requiere un proceso de límite cuando los puntos se acercan

Error 2: No simplificar antes de aplicar el límite

• Incorrecto: Intentar evaluar ${\lim }_{h\to 0}\frac{f(a+h)-f(a)}{h}$ directamente (da $\frac{0}{0}$)
• Correcto: Expandir, simplificar algebraicamente y luego aplicar el límite

Error 3: Confundir velocidad promedio con instantánea

• Incorrecto: Pensar que $\frac{f(5)-f(0)}{5}$ es la velocidad en $t=5$
• Correcto: La velocidad en $t=5$ es ${\lim }_{h\to 0}\frac{f(5+h)-f(5)}{h}$

Error 4: Olvidar las unidades físicas

• Incorrecto: Dar velocidad sin unidades
• Correcto: Si posición está en metros y tiempo en segundos, velocidad está en m/s

---

📝 Ejercicios Propuestos

Ejercicios de Práctica

1. Encuentre la ecuación de la recta tangente a $y=x^3$ en el punto $(2,8)$
2. Si $f(x)=\sqrt{x}$, calcule $f^{\prime }(4)$ usando la definición
3. Un objeto se mueve según $s(t)=t^3-6t^2$. Encuentre su velocidad en $t=2$
4. Demuestre que la tangente a $y=1/x$ en $(a,1/a)$ tiene ecuación $y=-\frac{1}{a^2}x+\frac{2}{a}$

---

📚 Referencias

Lectura Principal

• Sección 2.7: Derivadas y razones de cambio, págs. 143-146

Enlaces Relacionados

• 9) Limites al Infinito y Asintotas Horizontales - Conceptos prerequisito
• Recta-Tangente
• Velocidad-Instantanea
• Derivada

---

Sugerencia de Estudio

La derivada es el concepto central del cálculo diferencial. Domina las dos interpretaciones (geométrica como pendiente y física como velocidad) y practica el cálculo usando la definición con límites. Los ejemplos 1, 3 y 5 son fundamentales para comprender este concepto.

---

✅ Checklist de Estudio

Lista de Verificación

• Puedo explicar qué es una recta tangente usando el concepto de límite
• Entiendo la diferencia entre recta secante y tangente
• Sé calcular la pendiente de la tangente usando la definición
• Comprendo la relación entre posición, velocidad y derivada
• Puedo calcular derivadas usando la definición $f^{\prime }(a)={\lim }_{h\to 0}\frac{f(a+h)-f(a)}{h}$
• Distingo entre velocidad promedio e instantánea
• Puedo escribir la ecuación de una recta tangente conociendo la derivada
• Entiendo que la derivada unifica problemas geométricos y físicos

---

🏷️ Tags

calculo derivadas recta-tangente velocidad-instantanea velocidad-promedio razon-de-cambio limite clase-10 clase