11) Razón de Cambio Promedio y Razón de Cambio Instantánea

Clase 11: Razón de Cambio Promedio y Razón de Cambio Instantánea

📚 Introducción

Esta clase profundiza en la interpretación de la derivada como razón de cambio, ampliando la perspectiva física de la velocidad a contextos más generales de las ciencias naturales, sociales e ingeniería. Mientras que en la clase anterior vimos que la derivada representa la pendiente de la recta tangente y la velocidad de un objeto, ahora exploraremos cómo este mismo concepto matemático describe cambios instantáneos en diversas situaciones: crecimiento poblacional, costos de producción, reacciones químicas, y más.

Objetivos de la Clase

• Comprender el concepto de razón de cambio promedio de una cantidad respecto a otra
• Definir la razón de cambio instantánea como límite de razones promedio
• Interpretar la derivada como razón de cambio en diversos contextos
• Aplicar el concepto de razón de cambio a problemas de física, economía y otras ciencias
• Distinguir entre cambio promedio e instantáneo en situaciones reales

---

1. Razón de Cambio Promedio

1.1 Concepto General

Definición - Razón de Cambio Promedio

Suponga que $y$ es una cantidad que depende de otra cantidad $x$, es decir, $y=f(x)$.

Si $x$ cambia de $x_1$ a $x_2$, entonces:

• El cambio en $x$ (también llamado incremento de $x$) es: $\Delta x=x_2-x_1$
• El cambio correspondiente en $y$ es: $\Delta y=f(x_2)-f(x_1)$

El cociente de diferencias

$\frac{\Delta y}{\Delta x}=\frac{f(x_2)-f(x_1)}{x_2-x_1}$

se llama razón de cambio promedio de $y$ respecto a $x$ sobre el intervalo $[x_1,x_2]$.

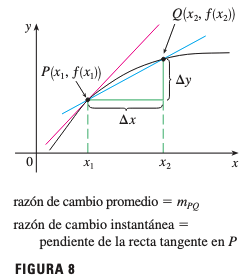
Interpretación Geométrica

La razón de cambio promedio puede interpretarse como la pendiente de la recta secante $PQ$ que une los puntos $P(x_1,f(x_1))$ y $Q(x_2,f(x_2))$ en la gráfica de $f$.

1.2 Notación Delta (Δ)

La letra griega Δ (delta mayúscula) se usa tradicionalmente para denotar “cambio en”:

• $\Delta x$ se lee “delta x” y significa “cambio en x”
• $\Delta y$ se lee “delta y” y significa “cambio en y”

Precaución

$\Delta x$ NO significa “delta por x”. Es un símbolo único que representa el incremento o cambio en la variable $x$.

---

2. Razón de Cambio Instantánea

2.1 Del Promedio al Instantáneo

Por analogía con la velocidad, consideramos la razón de cambio promedio en intervalos cada vez más pequeños haciendo que $x_2$ tienda a $x_1$ (o equivalentemente, que $\Delta x\to 0$).

Definición - Razón de Cambio Instantánea

La razón de cambio instantánea de $y=f(x)$ respecto a $x$ cuando $x=x_1$ es:

${\lim }_{\Delta x\to 0}\frac{\Delta y}{\Delta x}={\lim }_{x_2\to x_1}\frac{f(x_2)-f(x_1)}{x_2-x_1}$

Reconocemos este límite: ¡Es precisamente la derivada $f^{\prime }(x_1)$!

Interpretación Fundamental

La derivada $f^{\prime }(a)$ representa tres conceptos equivalentes:

1. Geométrica: Pendiente de la recta tangente en $(a,f(a))$
2. Física: Velocidad instantánea (cuando $f$ representa posición)
3. General: Razón de cambio instantánea de $y$ respecto a $x$ cuando $x=a$

2.2 Relación Visual

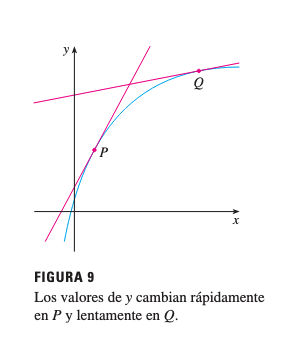
Conforme $\Delta x\to 0$:

• La razón de cambio promedio $\to$ razón de cambio instantánea
• La pendiente de la recta secante $\to$ pendiente de la recta tangente
• El cociente $\frac{\Delta y}{\Delta x}\to f^{\prime }(x_1)$

---

3. Aplicaciones en Ciencias Naturales

3.1 Física: Velocidad y Aceleración

Ya hemos visto que si $s=f(t)$ es la función posición de un objeto:

• Velocidad instantánea:

$v(t)=\frac{ds}{dt}=f^{\prime }(t)$

• Aceleración instantánea:

$a(t)=\frac{dv}{dt}=v^{\prime }(t)=f^{\prime \prime }(t)$

Interpretación Física

• La velocidad es la razón de cambio de la posición respecto al tiempo
• La aceleración es la razón de cambio de la velocidad respecto al tiempo

3.2 Química: Velocidad de Reacción

En química, si $C(t)$ representa la concentración de un reactivo en el tiempo $t$:

Velocidad de reacción =

$-\frac{dC}{dt}=-C^{\prime }(t)$

(El signo negativo indica que la concentración disminuye)

3.3 Biología: Crecimiento Poblacional

Si $P(t)$ es la población en el tiempo $t$:

Tasa de crecimiento poblacional =

$\frac{dP}{dt}=P^{\prime }(t)$

---

4. Aplicaciones en Economía

4.1 Costo Marginal

Definición - Costo Marginal

Si $C(x)$ es el costo de producir $x$ unidades de cierto artículo, entonces el costo marginal es la derivada:

$C^{\prime }(x)=\frac{dC}{dx}$

Representa la razón de cambio del costo de producción respecto al número de unidades producidas.

4.2 Ejemplo 6: Fabricante de Tejidos

Problema: Un fabricante produce un rollo de un tejido con ancho fijo. El costo de producir $x$ yardas de este tejido es de $C=f(x)$ dólares.

a) ¿Cuál es el significado de la derivada $f^{\prime }(x)$? ¿Cuáles son sus unidades? b) En términos prácticos, ¿qué significa decir que $f^{\prime }(1000)=9$? c) ¿Cuál piensa que es más grande $f^{\prime }(50)$ o $f^{\prime }(500)$? ¿Qué hay respecto a $f^{\prime }(5000)$?

Solución

Parte a): Significado de $f^{\prime }(x)$

La derivada $f^{\prime }(x)$ es la razón de cambio instantánea de $C$ respecto a $x$, es decir:

$f^{\prime }(x)={\lim }_{\Delta x\to 0}\frac{\Delta C}{\Delta x}$

Esto representa la razón de cambio del costo de producción respecto al número de yardas producidas. Los economistas llaman a esta rapidez de cambio costo marginal.

Unidades: Puesto que $\Delta C$ se mide en dólares y $\Delta x$ en yardas, las unidades para $f^{\prime }(x)$ son:

$\text{doˊlares por cada yarda}$

Parte b): Interpretación de $f^{\prime }(1000)=9$

El enunciado $f^{\prime }(1000)=9$ significa que, después de fabricar 1000 yardas de tejido, la cantidad a la cual se incrementa el costo de producción es de 9 dólares por yarda.

Cuando $x=1000$, $C$ se incrementa 9 veces tan rápido como $x$.

Dado que $\Delta x=1$ es pequeño si se le compara con $x=1000$, podría usarse la aproximación:

$f^{\prime }(1000)\approx \frac{\Delta C}{\Delta x}=\frac{\Delta C}{1}=\Delta C$

y decimos que el costo de fabricación de las 1000 yardas (o de la 1001) es de casi 9 dólares.

Parte c): Comparación de costos marginales

La razón a la cual se incrementa el costo de producción (por cada yarda) probablemente es inferior cuando $x=500$ que cuando $x=50$ (el costo de fabricación de la yarda 500 es menor que el costo de la yarda 50) debido a la escala económica. (El fabricante hace más eficiente el uso de los costos de producción fijos.)

De este modo:

$f^{\prime }(50)>f^{\prime }(500)$

Pero, conforme se expande la producción, el resultado de la operación a gran escala será ineficiente y con eso los costos de horas extra de trabajo. En estos términos, es posible que la razón de incremento de costos empezarán con el tiempo a subir. De este modo, es posible que suceda que:

$f^{\prime }(5000)>f^{\prime }(500)$

Observación Económica

En economía, el costo marginal suele tener forma de “U”:

• Decrece inicialmente (economías de escala)
• Alcanza un mínimo
• Luego aumenta (deseconomías de escala, horas extras, etc.)

4.3 Otras Razones Marginales en Economía

• Ingreso marginal: $R^{\prime }(x)$ = razón de cambio del ingreso total
• Ganancia marginal: $P^{\prime }(x)$ = razón de cambio de la ganancia
• Demanda marginal: Razón de cambio de la cantidad demandada respecto al precio

---

5. Ejemplo con Datos Tabulados

5.1 Ejemplo 7: Deuda Nacional de EE.UU.

Problema: Sea $D(t)$ la deuda nacional de EU en el tiempo $t$. La tabla proporciona valores aproximados de esta función desde 1980 hasta 2005. Interprete y estime el valor de $D^{\prime }(1990)$.

$t$	$D(t)$
1980	930.2
1985	1945.9
1990	3233.3
1995	4974.0
2000	5674.2
2005	7932.7

Solución

Interpretación: La derivada $D^{\prime }(1990)$ significa la razón de cambio de $D$ respecto a $t$ cuando $t=1990$, es decir, la razón de incremento de la deuda nacional en 1990.

Estimación usando diferencias:

De acuerdo con la ecuación 5:

$D^{\prime }(1990)={\lim }_{t\to 1990}\frac{D(t)-D(1990)}{t-1990}$

Calculamos el cociente de diferencias (la razón de cambio promedio) como sigue:

$t$	$\frac{D(t)-D(1990)}{t-1990}$
1980	230.31
1985	257.48
1995	348.14
2000	244.09
2005	313.29

A partir de esta tabla vemos que $D^{\prime }(1990)$ se localiza en alguna parte entre 257.48 y 348.14 miles de millones de dólares por cada año.

[En este caso, está haciendo la suposición razonable de que la deuda no fluctuó de manera errática entre 1980 y el 2000.]

Se estima que la razón de incremento de la deuda nacional de EU en 1990 fue el promedio de estos números:

$D^{\prime }(1990)\approx 303\text{ miles de millones de doˊlares por cada an˜o}$

Nota sobre Unidades

Las unidades de la razón de cambio instantánea $\Delta D/\Delta t$ son las mismas que las unidades para el cociente de diferencias $\Delta D/\Delta t$. Puesto que $\Delta D$ se mide en miles de millones de dólares y $\Delta t$ en años, las unidades para $D^{\prime }(t)$ son miles de millones de dólares por cada año.

---

6. Resumen de Interpretaciones de la Derivada

Tres Interpretaciones Equivalentes de f'(a)

1. Geométrica: Pendiente de la recta tangente a $y=f(x)$ en $x=a$
2. Cinemática: Velocidad instantánea cuando $f$ representa posición
3. Razón de cambio: Razón de cambio instantánea de $y$ respecto a $x$ en $x=a$

El poder de la derivada radica en que unifica todos estos conceptos bajo una misma estructura matemática.

---

🎯 Conceptos Clave para Repasar

Resumen de Conceptos

1. Razón de cambio promedio: $\frac{\Delta y}{\Delta x}=\frac{f(x_2)-f(x_1)}{x_2-x_1}$ (pendiente de recta secante)
2. Razón de cambio instantánea: ${\lim }_{\Delta x\to 0}\frac{\Delta y}{\Delta x}=f^{\prime }(x_1)$ (derivada)
3. Costo marginal: $C^{\prime }(x)$ = razón de cambio del costo respecto a unidades producidas
4. Unidades de la derivada: Si $y$ se mide en unidades A y $x$ en unidades B, entonces $f^{\prime }(x)$ se mide en “A por cada B”
5. Interpretación práctica: La derivada mide “qué tan rápido” cambia una cantidad
6. Estimación con datos: Usar razones de cambio promedio para aproximar derivadas

---

🚨 Errores Comunes

Error 1: Confundir razón promedio con instantánea

• Incorrecto: Decir que $\frac{f(5)-f(0)}{5}$ es la razón de cambio en $t=5$
• Correcto: Eso es la razón promedio en $[0,5]$; la instantánea en $t=5$ es $f^{\prime }(5)$

Error 2: Ignorar las unidades

• Incorrecto: Decir que $C^{\prime }(100)=5$ sin especificar unidades
• Correcto: $C^{\prime }(100)=5$ dólares/unidad (si $C$ está en dólares y $x$ en unidades)

Error 3: Malinterpretar el costo marginal

• Incorrecto: Pensar que $C^{\prime }(1000)=9$ significa que 1000 unidades cuestan $9
• Correcto: Significa que la unidad 1001 cuesta aproximadamente $9 adicionales

Error 4: Olvidar que Δx NO es multiplicación

• Incorrecto: Separar Δ y x como si fueran factores
• Correcto: $\Delta x$ es un símbolo único que significa “cambio en x”

---

📝 Ejercicios Propuestos

Ejercicios de Práctica

1. Un tanque contiene 5000 litros de agua pura. Salmuera con 30 g/L de sal entra a razón de 25 L/min. Si $Q(t)$ es la cantidad de sal después de $t$ minutos, encuentre la razón de cambio de sal en $t=5$ min
2. El costo de producir $x$ onzas de oro es $C(x)=500+3x+0.01x^2$ dólares. Encuentre el costo marginal cuando se han producido 50 onzas
3. Una población de bacterias crece según $P(t)=1000e^{0.3t}$. ¿A qué razón crece la población cuando $t=2$ horas?
4. Si el radio de una esfera aumenta a razón de 2 cm/s, ¿a qué razón aumenta el volumen cuando $r=10$ cm?

---

📚 Referencias

Lectura Principal

• Sección 2.7: Derivadas y razones de cambio, págs. 147-150

Enlaces Relacionados

• 10) Recta Tangente, Velocidad y el Concepto de Derivada - Clase anterior
• Razon-de-Cambio
• Costo-Marginal
• Derivada

---

Sugerencia de Estudio

La clave está en comprender que la derivada NO es solo un concepto matemático abstracto, sino una herramienta para medir “qué tan rápido cambia algo”. Ya sea velocidad de un auto, costo de producción, o crecimiento poblacional, la derivada cuantifica la razón de cambio. Practicar identificando las unidades de la derivada te ayudará a entender mejor su significado en cada contexto.

---

✅ Checklist de Estudio

Lista de Verificación

• Comprendo la diferencia entre razón de cambio promedio e instantánea
• Puedo calcular razones de cambio promedio usando $\frac{\Delta y}{\Delta x}$
• Entiendo que la razón de cambio instantánea es la derivada
• Sé interpretar el significado de la derivada en diferentes contextos
• Puedo determinar las unidades correctas de una derivada
• Comprendo el concepto de costo marginal en economía
• Puedo estimar derivadas a partir de datos tabulados
• Reconozco cuándo usar razón promedio vs instantánea en problemas aplicados

---

🏷️ Tags

calculo derivadas razon-de-cambio razon-cambio-promedio razon-cambio-instantanea costo-marginal aplicaciones-derivadas economia fisica clase-11 clase