21) Valores Maximos y Minimos

Clase 21: Valores Máximos y Mínimos

📚 Introducción

En las aplicaciones del cálculo diferencial, uno de los problemas más importantes es encontrar los valores óptimos de una función. Ya sea maximizar ganancias, minimizar costos, o encontrar la mejor forma para un diseño, todos estos problemas se reducen a encontrar valores máximos y mínimos de funciones. En esta clase, aprenderemos a identificar y clasificar estos valores extremos, sentando las bases para los problemas de optimización.

Objetivos de la Clase

• Comprender y diferenciar los conceptos de mínimo (máximo) local y absoluto
• Determinar valores de mínimo (máximo) local y absoluto de una función conociendo su gráfica
• Comprender la necesidad de cada hipótesis en el Teorema del Valor Extremo
• Conocer el Teorema de Fermat e identificar que el recíproco no siempre es cierto
• Calcular números críticos de una función
• Relacionar números críticos con mínimos, máximos y puntos engañosos (ni lo uno ni lo otro)

---

1. Valores Máximos y Mínimos

1.1 Definiciones Fundamentales

Definición - Valor Máximo Absoluto

Sea $c$ un número en el dominio $D$ de una función $f$. Entonces $f(c)$ es el valor máximo absoluto de $f$ sobre $D$ si:

$f(c)\ge f(x)\text{ para toda }x\in D$

Definición - Valor Mínimo Absoluto

Sea $c$ un número en el dominio $D$ de una función $f$. Entonces $f(c)$ es el valor mínimo absoluto de $f$ sobre $D$ si:

$f(c)\le f(x)\text{ para toda }x\in D$

Nomenclatura Alternativa

Los valores máximo y mínimo absolutos también se conocen como valores extremos absolutos o simplemente valores extremos de la función.

1.2 Valores Máximos y Mínimos Locales

Definición - Máximo Local

El número $f(c)$ es un valor máximo local de $f$ si:

$f(c)\ge f(x)\text{ cuando }x\text{ estaˊ cerca de }c$

Formalmente, esto significa que existe un intervalo abierto que contiene a $c$ tal que $f(c)\ge f(x)$ para toda $x$ en ese intervalo.

Definición - Mínimo Local

El número $f(c)$ es un valor mínimo local de $f$ si:

$f(c)\le f(x)\text{ cuando }x\text{ estaˊ cerca de }c$

Diferencia Clave

• Máximos y mínimos locales solo pueden ocurrir en un punto interior del dominio
• Si el dominio es un intervalo cerrado, entonces no pueden ocurrir en los extremos del intervalo
• Máximos y mínimos absolutos pueden ocurrir en cualquier punto del dominio

1.3 Ejemplos Visuales

Ejemplo 1: La función coseno

La función $f(x)=\cos x$ toma su valor máximo (local y absoluto) igual a $1$ infinitas veces, ya que $\cos 2n\pi =1$ para cualquier entero $n$, y $1\ge \cos x\ge -1$ para todo $x$.

Del mismo modo, $\cos (2n+1)\pi =-1$ es su valor mínimo, donde $n$ es cualquier entero.

Ejemplo 2: La función cuadrática

$f(x)=x^2$ Para $f(x)=x^2$, tenemos que $f(x)\ge f(0)$ porque $x^2\ge 0$ para toda $x$. Por tanto, $f(0)=0$ es el valor mínimo absoluto (y local) de $f$.

Esta función corresponde al hecho de que el origen es el punto más bajo sobre la parábola $y=x^2$.

Sin embargo, no existe el punto más alto sobre la parábola, por lo que esta función no tiene valor máximo.

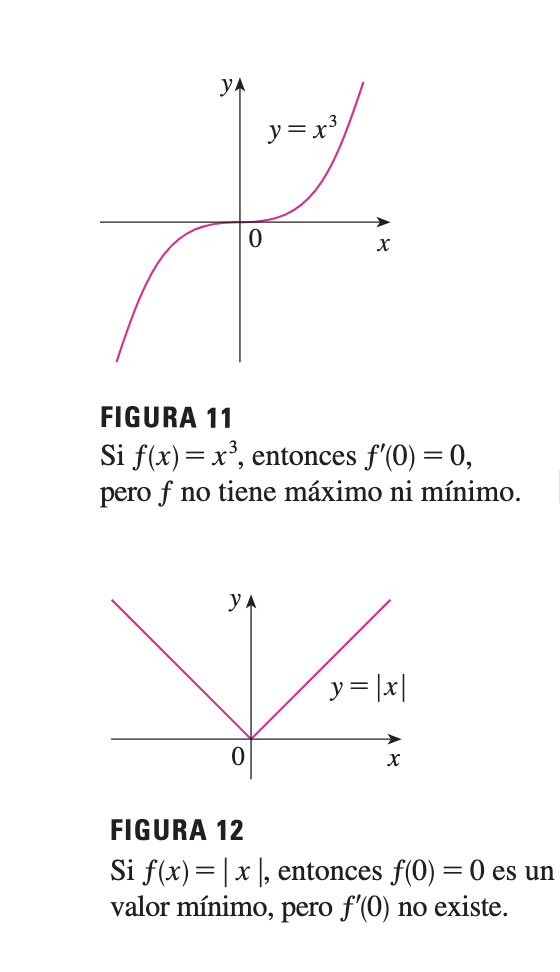
Ejemplo 3: La función cúbica

$f(x)=x^3$ Para la función $f(x)=x^3$, la gráfica muestra que no tiene valor máximo absoluto ni valor mínimo absoluto. De hecho, tampoco posee valores extremos locales.

---

2. El Teorema del Valor Extremo

2.1 Condiciones para la Existencia de Extremos

Teorema del Valor Extremo

Si $f$ es continua sobre un intervalo cerrado $[a,b]$, entonces $f$ alcanza un valor máximo absoluto $f(c)$ y un valor mínimo absoluto $f(d)$ en algunos números $c$ y $d$ en $[a,b]$.

Advertencia sobre las Hipótesis

Los ejemplos siguientes advierten contra la interpretación excesiva del Teorema del Valor Extremo. No podemos esperar localizar valores extremos haciendo simplemente $f^{\prime }(x)=0$ y resolviendo para $x$.

2.2 Funciones que NO Tienen Valores Extremos

Ejemplo: Función continua en intervalo abierto

Una función continua sobre un intervalo abierto podría no tener valores extremos.

Ejemplo: La función cuya gráfica se muestra está definida sobre el intervalo cerrado $[0,2]$, pero no tiene valor máximo. (El rango de esta función es $[0,3)$).

Nota: Los máximos y mínimos absolutos pueden ocurrir en cualquier punto del dominio, pero los máximos y mínimos locales solo pueden ocurrir en un punto interior del dominio. En particular, si el dominio es un intervalo cerrado, entonces no pueden ocurrir en los extremos del intervalo.

Ejemplo: Función discontinua

Esta función continua $g$ que se muestra no tiene valor máximo ni mínimo, ya que el rango de $g$ es $(1,\infty )$. La función toma valores arbitrariamente grandes.

Conclusión: Una función discontinua puede tener valores máximo y mínimo. (Véase el ejercicio 13b.)

---

3. El Teorema de Fermat

3.1 Relación entre Extremos Locales y Derivadas

En la figura del texto se muestra la gráfica de una función $f$ con un máximo local en $c$ y un mínimo local en $d$. Parece que en los puntos máximo y mínimo la recta tangente es horizontal y, por consiguiente, tiene pendiente $0$. Sabemos que la derivada es la pendiente de la recta tangente, de modo que parece que $f^{\prime }(c)=0$ y $f^{\prime }(d)=0$.

Teorema de Fermat

Si $f$ tiene un máximo o un mínimo local en $c$, y si $f^{\prime }(c)$ existe, entonces:

$f^{\prime }(c)=0$

Precaución - El Recíproco NO es Siempre Cierto

Los ejemplos 5 y 6 demuestran que debe ser cuidadoso al aplicar el Teorema de Fermat. El ejemplo 5 demuestra que aun cuando $f^{\prime }(a)=0$, no necesariamente hay un máximo o un mínimo en $a$. (En otras palabras, el inverso del Teorema de Fermat es en general falso.)

Podría haber un valor extremo aun cuando $f^{\prime }(c)$ no exista (como en la figura 12).

3.2 Demostración del Teorema de Fermat (para el caso de máximo local)

Demostración

Suponga que $f$ tiene un máximo local en $c$. Entonces, según la definición 2, $f(c)\ge f(x)$ si $x$ es suficientemente cercana a $c$. Esto implica que si $h>0$ y es suficientemente pequeña, tenemos:

$f(c)\ge f(c+h)$

y, por consiguiente:

$\frac{f(c+h)-f(c)}{h}\le 0$

Podemos dividir ambos lados de la desigualdad entre un número positivo. Así, si $h>0$ y $h$ es suficientemente pequeña, tenemos:

$\frac{f(c+h)-f(c)}{h}\le 0$

Tomando el límite por la derecha de ambos lados de la desigualdad (utilizando el teorema 2.3.2), obtenemos:

${\lim }_{h\to 0^{+}}\frac{f(c+h)-f(c)}{h}\le {\lim }_{h\to 0^{+}}0=0$

Pero, dado que $f^{\prime }(c)$ existe, tenemos:

$f^{\prime }(c)={\lim }_{h\to 0}\frac{f(c+h)-f(c)}{h}={\lim }_{h\to 0^{+}}\frac{f(c+h)-f(c)}{h}$

y con esto se demuestra que $f^{\prime }(c)\le 0$.

Si $h<0$, entonces la dirección de la desigualdad se invierte cuando dividimos por $h$:

$\frac{f(c+h)-f(c)}{h}\ge 0\text{para }h<0$

Así que tomando el límite por la izquierda, tenemos:

$f^{\prime }(c)={\lim }_{h\to 0^{-}}\frac{f(c+h)-f(c)}{h}\ge {\lim }_{h\to 0^{-}}0=0$

Ya hemos mostrado que $f^{\prime }(c)\le 0$ y también que $f^{\prime }(c)\ge 0$. Puesto que ambas desigualdades deben ser verdaderas, la única posibilidad es que $f^{\prime }(c)=0$.

El caso de un mínimo local puede demostrarse de modo similar, o bien, puede usar el ejercicio 76 para deducirlo del caso que ya ha demostrado (véase el ejercicio 77).

3.3 Ejemplos de Aplicación del Teorema de Fermat

Ejemplo 5:

$f(x)=x^3$ Si $f(x)=x^3$, entonces $f^{\prime }(x)=3x^2$, de modo que $f^{\prime }(0)=0$. Pero $f$ no tiene máximo o mínimo en $x=0$, como puede ver en la gráfica. (O bien, observe que $x^3>0$ para $x>0$ pero $x^3<0$ para $x<0$.)

El hecho de que $f^{\prime }(0)=0$ solo significa que la curva $y=x^3$ tiene una recta tangente horizontal en $(0,0)$. En lugar de tener un máximo o un mínimo en $(0,0)$, allí cruza la curva su recta tangente horizontal.

Ejemplo 6:

$f(x)=|x|$ La función $f(x)=|x|$ muestra un valor mínimo (local y absoluto) en $x=0$, pero ese valor no puede determinarse haciendo $f^{\prime }(x)=0$ porque, como ya se demostró en el ejemplo 5 de la sección 2.8, $f^{\prime }(0)$ no existe (véase la figura).

Precaución: Aun cuando $f^{\prime }(c)=0$, no necesariamente hay un máximo o un mínimo en $c$. (En otras palabras, el inverso del Teorema de Fermat es en general falso.)

Además, podría haber un valor extremo aun cuando $f^{\prime }(c)$ no exista (como en el ejemplo 6).

---

4. Números Críticos

4.1 Definición de Número Crítico

El Teorema de Fermat sugiere que, por lo menos, debe empezar a buscar los valores extremos de $f$ en los números $x=c$, donde $f^{\prime }(c)=0$ o donde $f^{\prime }(c)$ no existe. Estos números reciben un nombre especial.

Definición - Número Crítico

Un número crítico de una función $f$ es un número $c$ en el dominio de $f$ tal que:

$f^{\prime }(c)=0\text{o}{f}^{\prime }(c)\text{ no existe}$

Teorema 6 - Relación entre Números Críticos y Extremos

Si $f$ tiene un máximo o un mínimo local en $c$, entonces $c$ es un número crítico de $f$.

Método para Hallar Valores Extremos

Para hallar un máximo o mínimo absolutos de una función continua $f$ sobre un intervalo cerrado $[a,b]$:

1. Encuentre los valores de $f$ en los números críticos de $f$ en $(a,b)$
2. Halle los valores de $f$ en los puntos extremos del intervalo
3. El más grande de los valores de los pasos 1 y 2 es el valor máximo absoluto; el más pequeño, el valor mínimo absoluto

4.2 Ejemplos de Números Críticos

Ejemplo 7: Encontrar números críticos

Encuentre los números críticos de $f(x)=x^{3/5}(4-x)$.

Solución: La regla del producto nos da:

$f^{\prime }(x)=x^{3/5}(-1)+(4-x)\left(\frac{3}{5}{x}^{-2/5}\right)=-x^{3/5}+\frac{3(4-x)}{5x^{2/5}}$

$=\frac{-5x+3(4-x)}{5x^{2/5}}=\frac{12-8x}{5x^{2/5}}$

[Se obtienen los mismos valores escribiendo primero $f(x)=4x^{3/5}-x^{8/5}$.] Así que $f^{\prime }(x)=0$ si $12-8x=0$; es decir $x=\frac{3}{2}$ y $f^{\prime }(x)$ no existe cuando $x=0$. Por tanto, los números críticos son $\frac{3}{2}$ y $0$.

Ejemplo 8: Valores extremos absolutos

Encuentre los valores absolutos máximo y mínimo de la función:

$f(x)=x^3-3x^2+1\text{para }-\frac{1}{2}\le x\le 4$

Solución: Dado que $f$ es continua sobre $\left[-\frac{1}{2},4\right]$, podemos utilizar el teorema del intervalo cerrado:

$f(x)=x^3-3x^2+1$ $f^{\prime }(x)=3x^2-6x=3x(x-2)$

Puesto que $f^{\prime }(x)$ existe para toda $x$, los únicos valores críticos de $f$ ocurren cuando $f^{\prime }(x)=0$; esto es, en $x=0$ o $x=2$. Observe que cada uno de estos números críticos está en el intervalo $\left[-\frac{1}{2},4\right]$. Los valores de $f$ en estos números críticos son:

$f(0)=1f(2)=-3$

Los valores de $f$ en los puntos extremos del intervalo son:

$f\left(-\frac{1}{2}\right)=\frac{1}{8}f(4)=17$

Comparando estos cuatro números, vemos que el valor máximo absoluto es $f(4)=17$ y el valor mínimo absoluto es $f(2)=-3$.

---

🎯 Conceptos Clave para Repasar

Resumen de Conceptos

1. Valor máximo absoluto: $f(c)\ge f(x)$ para toda $x$ en el dominio
2. Valor mínimo absoluto: $f(c)\le f(x)$ para toda $x$ en el dominio
3. Valor máximo local: $f(c)\ge f(x)$ cuando $x$ está cerca de $c$
4. Valor mínimo local: $f(c)\le f(x)$ cuando $x$ está cerca de $c$
5. Teorema del Valor Extremo: Función continua en intervalo cerrado → tiene máximo y mínimo absolutos
6. Teorema de Fermat: Si $f$ tiene extremo local en $c$ y $f^{\prime }(c)$ existe → $f^{\prime }(c)=0$
7. Número crítico: Punto donde $f^{\prime }(c)=0$ o $f^{\prime }(c)$ no existe
8. Los extremos locales solo ocurren en puntos interiores del dominio
9. Los extremos absolutos pueden ocurrir en cualquier punto del dominio

---

🚨 Errores Comunes

Error 1: Confundir local con absoluto

• Incorrecto: Pensar que todo máximo local es máximo absoluto
• Correcto: Un máximo local solo es el mayor valor en una vecindad del punto

Error 2: Aplicar mal el Teorema de Fermat

• Incorrecto: Si $f^{\prime }(c)=0$, entonces hay un extremo en $c$
• Correcto: Si hay un extremo en $c$, entonces $f^{\prime }(c)=0$ o no existe. El recíproco es falso.

Error 3: Olvidar los puntos donde la derivada no existe

• Incorrecto: Solo buscar donde $f^{\prime }(x)=0$ para números críticos
• Correcto: Los números críticos incluyen tanto donde $f^{\prime }(c)=0$ como donde $f^{\prime }(c)$ no existe

Error 4: No verificar los extremos del intervalo

• Incorrecto: Solo evaluar en números críticos interiores
• Correcto: También evaluar $f(a)$ y $f(b)$ en los extremos del intervalo $[a,b]$

Error 5: Asumir que toda función continua tiene extremos

• Incorrecto: Pensar que cualquier función continua tiene máximo y mínimo
• Correcto: Se necesita continuidad Y un intervalo cerrado según el Teorema del Valor Extremo

---

📝 Ejercicios Propuestos

Ejercicios de Práctica

Ejercicios del libro (Sección 4.1, págs. 274-278):

1. Ejemplo 4, pág. 275: Estudiar valores extremos en gráficas dadas

2. Ejercicio sobre $x^3,x^2$ y $|x|$ en $x=0$ para el Teorema de Fermat

3. Ejemplo 7, pág. 278: Encontrar números críticos de funciones con raíces

4. Determine si las siguientes afirmaciones son verdaderas o falsas:

   • Si $f^{\prime }(c)=0$, entonces $f$ tiene un extremo local en $c$
   • Si $f$ es continua en $[a,b]$, entonces $f$ tiene un máximo absoluto
   • Si $f$ tiene un máximo en $c$, entonces $f^{\prime }(c)=0$

5. Para $f(x)=x^4-2x^2+3$ en $[-2,3]$:

   • Encuentre todos los números críticos
   • Determine los valores extremos absolutos

6. Encuentre los números críticos de $g(x)=|3x-4|$

---

📚 Referencias

Lectura Principal

• Sección 4.1: Valores máximos y mínimos, págs. 274-278
• Stewart, James. “Cálculo de una Variable: Trascendentes Tempranas”, 7ª edición

Ejercicios Recomendados

• Ejemplo 4, pág. 275
• Ejercicios sobre $x^3$, $x^2$ y $|x|$ en $x=0$ para el Teorema de Fermat
• Ejemplo 7, pág. 278

Enlaces Relacionados

• 20) Aproximaciones Lineales y Diferenciales - Conceptos prerequisito
• Teorema-Valor-Extremo
• Teorema-Fermat
• Numeros-Criticos

---

Nota Histórica: Pierre de Fermat

El Teorema de Fermat lleva ese nombre en honor de Pierre de Fermat (1601-1665), un abogado francés que tomó a las matemáticas como un pasatiempo. A pesar de su condición de aficionado, Fermat fue uno de los dos inventores de la geometría analítica (Descartes fue el otro). Sus métodos para hallar rectas tangentes a las curvas y valores máximos y mínimos (antes de la invención del límite y de las derivadas) lo hicieron un precursor de Newton en la creación del Cálculo Diferencial.

---

Sugerencia de Estudio

Este tema es fundamental para problemas de optimización. Practica identificando valores extremos tanto en gráficas como usando derivadas. Los ejemplos 4, 7 y 8 son esenciales. Recuerda que el Teorema de Fermat te dice dónde buscar extremos, pero no garantiza que existan. Siempre verifica evaluando la función en los puntos críticos y en los extremos del intervalo.

---

✅ Checklist de Estudio

Lista de Verificación

• Puedo distinguir entre valores extremos locales y absolutos
• Entiendo las dos hipótesis del Teorema del Valor Extremo (continuidad e intervalo cerrado)
• Sé que el Teorema de Fermat NO garantiza extremos si $f^{\prime }(c)=0$
• Puedo identificar números críticos (tanto donde $f^{\prime }(c)=0$ como donde no existe)
• Comprendo que los extremos locales solo ocurren en puntos interiores
• Sé aplicar el método del intervalo cerrado para encontrar extremos absolutos
• Puedo calcular derivadas y resolver $f^{\prime }(x)=0$
• Recuerdo evaluar la función en los extremos del intervalo
• Entiendo por qué $f(x)=x^3$ no tiene extremo en $x=0$ aunque $f^{\prime }(0)=0$
• Comprendo por qué $f(x)=|x|$ tiene mínimo en $x=0$ aunque $f^{\prime }(0)$ no existe

---

🏷️ Tags

calculo aplicaciones-derivada valores-extremos maximos-minimos teorema-valor-extremo teorema-fermat numeros-criticos optimizacion clase-21 clase